
【题目】已知点A(t,y1),B(t+2,y2)在抛物线![]() 的图象上,且﹣2≤t≤2,则线段AB长的最大值、最小值分别是( )
的图象上,且﹣2≤t≤2,则线段AB长的最大值、最小值分别是( )
A. 2![]() ,2B. 2
,2B. 2![]() ,2
,2![]() C. 2
C. 2![]() ,2D. 2
,2D. 2![]() ,2
,2![]()
【答案】C
【解析】
由点A、B在抛物线上,可用t表示y1、y2,根据两点间距离公式用t表示AB2,发现AB2与t是二次函数的关系,由抛物线性质和自变量t的取值范围可知:t在对称轴上时取得最小值;观察t本身的取值范围,看t=﹣2和t=2哪个离对称轴更远,即对应的函数值最大.
解:∵点A(t,y1),B(t+2,y2)在抛物线y=![]() 的图象上
的图象上
∴y1=![]()
∴AB2=(t+2﹣t)2+(y2﹣y1)2=22+![]() =4+(2t+2)2=4(t+1)2+4
=4+(2t+2)2=4(t+1)2+4
∴AB2与t是二次函数的关系,由抛物线性质可知:
当t=﹣1时,AB2取得最小值,AB2=4,AB=2
当t=2时,AB2取得最大值,AB2=4×(2+1)2+4=40,AB=2![]()
故选:C.


科目:初中数学 来源: 题型:
【题目】2019年4月22日是第50个世界地球日,某校在八年级5个班中,每班各选拔10名学生参加“环保知识竞赛”并评出了一、二、三等奖各若干名,学校将获奖情况绘成如图所示的不完整的条形统计图和扇形统计图,请你根据图中信息解答下列问题:

(1)求本次竞赛获奖的总人数,并补全条形统计图;
(2)求扇形统计图中“二等奖”所对应扇形的圆心角度数;
(3)如果该校八年级有800人,请你估计获奖的同学共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一次函数![]() 和反比例函数
和反比例函数![]() 的图象都经过点(1,1)(1)求反比例函数的解析式.(2)已知点
的图象都经过点(1,1)(1)求反比例函数的解析式.(2)已知点![]() 在第三象限,且同时在两个函数的图像上,求点
在第三象限,且同时在两个函数的图像上,求点![]() 的坐标.(3)利用(2)的结果,若点
的坐标.(3)利用(2)的结果,若点![]() 的坐标为(2,0),且以点
的坐标为(2,0),且以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形,请你直接写出点
为顶点的四边形是平行四边形,请你直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】结论开放某教研机构为了了解在校初中生阅读数学教科书的现状,随机抽取某校部分初中学生进行调查.依据所有调查数据绘制成以下不完整的统计图表,请根据图表中的信息解答下列问题:
类别 | 人数 | 占总人数的比例 |
重视 | a | 0.3 |
一般 | 57 | 0.38 |
不重视 | b | c |
说不清楚 | 9 | 0.06 |

(1)求样本容量及表格中a,b,c的值,并补全统计图.
(2)①根据上面的统计结果,谈谈你对该校初中生阅读数学教科书的现状的看法及建议;
②如果要了解全省初中生阅读数学教科书的情况,你认为应该如何进行抽样?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,按以下步骤作图:
①以B为圆心,任意长为半径作弧,分别交AB.BC于点M,N;②分别以M,N为圆心,以大于![]() MN的长为半径作弧,两弧相交于点E;③作射线BE;④用同样的方法作射线CF.BE交CF于点O.
MN的长为半径作弧,两弧相交于点E;③作射线BE;④用同样的方法作射线CF.BE交CF于点O.
请根据作图回答下列问题:
(1)O是△ABC的 ;
A.外心 B.内心 C.重心
(2)若AB=5,AC=12,BC=13,求O到BC的距离.
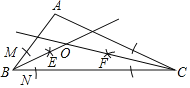
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳生活,绿色出行”是一种环保,健康的生活方式,小丽从甲地出发沿一条笔直的公路骑车前往乙地,她与乙地之间的距离y(km)与出发时间之间的函数关系式如图1中线段AB所示,在小丽出发的同时,小明从乙地沿同一条公路骑车匀速前往甲地,两人之间的距离S(km)与出发时间x(h)之间的函数关系式如图2中折线段CD-DE-EF所示.
(1)小丽和小明骑车的速度各是多少?
(2)求E点坐标,并解释点的实际意义.
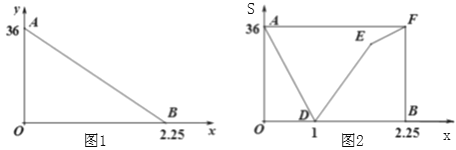
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于![]() BF的相同长度为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.若四边形ABEF的周长为16,∠C=60°,则四边形ABEF的面积是___.
BF的相同长度为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.若四边形ABEF的周长为16,∠C=60°,则四边形ABEF的面积是___.
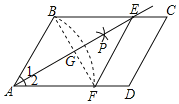
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把某矩形纸片ABCD沿EF、GH折叠(点E、H在AD边上,点F、G在BC边上),使得点B、点C落在AD边上同一点P处,A点的对称点为![]() 点,D点的对称点为
点,D点的对称点为![]() 点,若
点,若![]() ,
,![]() 的面积为4,
的面积为4,![]() 的面积为1,则矩形ABCD的面积等于_____.
的面积为1,则矩形ABCD的面积等于_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com