【题目】如图，己知正方形ABCD的边长为4, P是对角线BD上一点，PE⊥BC于点E, PF⊥CD于点F,连接AP, EF.给出下列结论:①PD=
EC:②四边形PECF的周长为8;③△APD一定是等腰三角形:④AP=EF；⑤EF的最小值为
；⑥AP⊥EF.其中正确结论的序号为（ ）
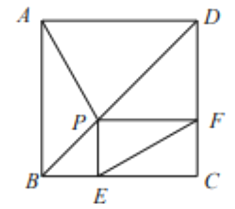
A. ①②④⑤⑥B. ①②④⑤
C. ②④⑤D. ②④⑤⑥
应用题天天练四川大学出版社系列答案科目：初中数学 来源： 题型：
【题目】已知M＝（a＋24）x3﹣10x2＋10x＋5是关于x的二次多项式，且二次项系数和一次项系数分别为b和c，在数轴上A、B、C三点所对应的数分别是a、b、c．
（1）则a＝ ，b＝ ，c＝ ．
（2）有一动点P从点A出发，以每秒4个单位的速度向右运动，多少秒后，P到A、B、C的距离和为40个单位？
（3）在（2）的条件下，当点P移动到点B时立即掉头，速度不变，同时点T和点Q分别从点A和点C出发，向左运动，点T的速度1个单位/秒，点Q的速度5个单位/秒，设点P、Q、T所对应的数分别是xP、xQ、xT，点Q出发的时间为t，当
＜t＜
时，求2|xP﹣xT|＋|xT﹣xQ|＋2|xQ﹣xP|的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）计算
① 8+(-1
)-6-(-1.25)；
②（
）×（﹣36）；
③﹣24+ 6×（﹣
）+（﹣6）×
；
④ 5+15÷(-3)2×[-(-1)4]-2.
（2）先化简，再求值：求 
的值，其中x﹦
,y = －1.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某中学库存若干套桌椅，准备修理后支援贫困山区学校。现有甲、乙两木工组，甲每天修理桌椅16套，乙每天修桌椅比甲多8套，甲单独修完这些桌椅比乙单独修完多用20天，学校每天付甲组80元修理费，付乙组120元修理费。
(1)该中学库存多少套桌椅？
(2)在修理过程中，学校要派一名工人进行质量监督，学校负担他每天10元生活补助费，现有三种修理方案:a、由甲单独修理；b、由乙单独修理；c、甲、乙合作同时修理。你认为哪种方案省时又省钱？为什么？
查看答案和解析>>
科目：初中数学 来源： 题型：
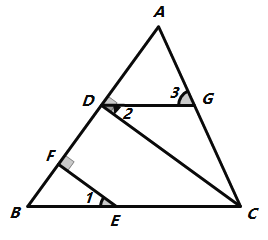
【题目】如图，在△ABC中，CD⊥AB，垂足为D. 点E在BC上，EF⊥AB，垂足为F，∠1=∠2.
(1)试说明DG∥BC的理由；
(2)如果∠B＝54°，且∠ACD=35°，求的∠3度数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】问题情境：如图1，AB∥CD，∠PAB=130°，∠PCD=120°，求∠APC的度数．
小明的思路是：过P作PE∥AB，通过平行线性质来求∠APC．
(1)按小明的思路，易求得∠APC的度数为_____度；
(2)问题迁移：如图2，AB∥CD，点P在射线OM上运动，记∠PAB=α，∠PCD=β，当点P在B、D两点之间运动时，问∠APC与α、β之间有何数量关系？请说明理由；
(3)在(2)的条件下，如果点P在B、D两点外侧运动时（点P与点O、B、D三点不重合），请直接写出∠APC与α、β之间的数量关系．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】先化简，再求值
（1）已知A=2x2-4xy-2x-3，B=-x2+xy+2，当x，y满足|x+1|+(y-2)2=0时，求A-
B的值；
（2）某同学做数学题“两个多项式A、B，B为4x2-5x-6，求A+B”时，误将A+B看成了A -B，求得的答案是-7x2+10x+12.
①请你写出A+B的正确答案；
②求当x=-3时，A+B的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商场销售A、B两种品牌的洗衣机,进价及售价如下表：
(1)该商场9月份用45000元购进A、B两种品牌的洗衣机，全部售完后获利9600元，求商场9月份购进A、B两种洗衣机的数量；
(2)该商场10月份又购进A、B两种品牌的洗衣机共用去36000元，
①问该商场共有几种进货方案?请你把所有方案列出来.
②通过计算说明洗衣机全部销售完后哪种进货方案所获得的利润最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
