考点:平行线分线段成比例
专题:计算题
分析:作ME∥AC交BD于E,NF∥AC交BD于F,如图,易得AD=CD,根据平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例由ME∥AD得
=
=
=
,同理由NF∥CD得到
=
=
,利用等式的性质得
=
,利用比例的性质得BE=
BD,BF=
BD,则EF=BF-BE=
BD,再利用ME∥NF得到
=
=
,所以OE=
EF=
BD,于是得到BO=BE+OE=
BD,OD=BD-BO=
BD,然后计算OD与OB的比.
解答: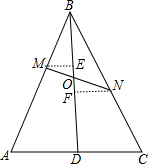
解:作ME∥AC交BD于E,NF∥AC交BD于F,如图,
∵BD为中线,
∴AD=CD,
∵ME∥AD,
=
,
∴
=
=
=
,
∵NF∥CD,
=
,
∴
=
=
,
∴
=
,BE=
BD,BF=
BD,
∴EF=BF-BE=
BD,
∵ME∥NF,
∴
=
=
,
∴OE=
EF=
BD,
∴BO=BE+OE=
BD,
∴OD=BD-BO=
BD,
∴
=
.
点评:本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例;平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例;如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边.

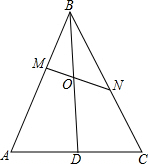 已知在△ABC中,
已知在△ABC中, 解:作ME∥AC交BD于E,NF∥AC交BD于F,如图,
解:作ME∥AC交BD于E,NF∥AC交BD于F,如图,

