
【提出问题】
(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
【类比探究】
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.


【考点】相似三角形的判定与性质;全等三角形的判定与性质;等边三角形的性质.
【分析】(1)利用SAS可证明△BAM≌△CAN,继而得出结论;
(2)也可以通过证明△BAM≌△CAN,得出结论,和(1)的思路完全一样.
(3)首先得出∠BAC=∠MAN,从而判定△ABC∽△AMN,得到
 =
=
 ,根据∠BAM=∠BAC﹣∠MAC,∠CAN=∠MAN﹣∠MAC,得到∠BAM=∠CAN,从而判定△BAM∽△CAN,得出结论.
,根据∠BAM=∠BAC﹣∠MAC,∠CAN=∠MAN﹣∠MAC,得到∠BAM=∠CAN,从而判定△BAM∽△CAN,得出结论.
【解答】(1)证明:∵△ABC、△AMN是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAM=∠CAN,
∵在△BAM和△CAN中,


∴△BAM≌△CAN(SAS),
∴∠ABC=∠ACN.
(2)解:结论∠ABC=∠ACN仍成立;
理由如下:∵△ABC、△AMN是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAM=∠CAN,
∵在△BAM和△CAN中,


∴△BAM≌△CAN(SAS),
∴∠ABC=∠ACN.
(3)解:∠ABC=∠ACN;
理由如下:∵BA=BC,MA=MN,顶角∠ABC=∠AMN,
∴底角∠BAC=∠MAN,
∴△ABC∽△AMN,
∴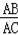
 =
=
 ,
,
又∵∠BAM=∠BAC﹣∠MAC,∠CAN=∠MAN﹣∠MAC,
∴∠BAM=∠CAN,
∴△BAM∽△CAN,
∴∠ABC=∠ACN.
【点评】本题考查了相似三角形的判定与性质、全等三角形的判定与性质,解答本题的关键是仔细观察图形,找到全等(相似)的条件,利用全等(相似)的性质证明结论.


科目:初中数学 来源: 题型:
若a>b,且c为实数,有下列各式:
①ac>bc;②ac<bc;③ac2>bc2;④ac2≥bc2;⑤
 >
>

其中,正确的有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
(1)求证:EB=EC;
(2)若以点O、D、E、C为顶点的四边形是正方形,试判断△ABC的形状,并说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
国家体育场“鸟巢”建筑面积达258000平方米,258000用科学记数法表示应为( )
A.2.58×103 B.25.8×104 C.2.58×105 D.258×103
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com