
【题目】如图,矩形ABCD中,![]() ,
,![]() ,动点P从点A出发,在AC上以每秒5cm的速度向点C匀速运动,同时动点Q从点D出发,在DA边上以每秒4cm的速度向点A匀速运动,运动时间为t秒(
,动点P从点A出发,在AC上以每秒5cm的速度向点C匀速运动,同时动点Q从点D出发,在DA边上以每秒4cm的速度向点A匀速运动,运动时间为t秒(![]() ),连接PQ.
),连接PQ.
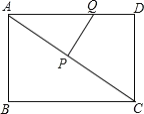
(1)若△APQ与△ADC相似,求t的值;
(2)连结CQ,DP,若![]() ,求t的值;
,求t的值;
(3)连结BQ,PD,请问BQ能和PD平行吗?若能,求出t的值:若不能,说明理由.
【答案】(1)![]() 或
或![]() ;
;
(2)![]() ;
;
(3)不存在这样的t,理由见详解.
【解析】
1)根据相似三角形对应边成比例,即可得到结论;
(2)过P作PM⊥AD于M,根据相似三角形的性质列比例式求得PM=3t,AM=4t,MD=8-4t,根据已知条件推出△PMD∽△QDC,根据相似三角形的性质列方程即可得到结论;
(3)设DP交BC于N,根据相似三角形的性质列比例式求得![]() ,得到
,得到![]() ,当BQ∥DP,得到四边形BQDN是平行四边形,根据平行四边形的性质列方程即可得到结论.
,当BQ∥DP,得到四边形BQDN是平行四边形,根据平行四边形的性质列方程即可得到结论.
解:(1)由题意得;QD=4t,AQ=8-4t,AP=5t,PC=10-t,
∵△APQ与△ADC相似,
∴情况①,当![]() 时,
时,![]() ,
,
即:![]() ,解得:
,解得:![]() ;
;
情况②当![]() 时,
时,![]() ,
,
即:![]() ,解得:
,解得:![]() ,
,
∴△APQ与△ADC相似时,![]() 或
或![]() ;
;
(2)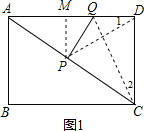
如图1,过P作PM⊥AD于M,
∵∠ADC=90°,
∴PM∥CD,
∴△APM∽△ACD,,
∴![]() ,
,
∵AP=5t,
∴![]()
∴化简得出:PM=3t,AM=4t,MD=8-4t,
∵CQ⊥DP,∴∠1=∠2,
∵∠PMD=∠CDQ=90°,
∴△PMD∽△QDC,
∴![]() ,即:
,即:![]()
解得:![]() ;
;
(3)
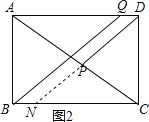
设DP交BC于N,
∴依题意得:![]() ,
,![]() ,
,
∵AD∥BC,
∴△ADP∽△CNP,
∴![]()
∴![]() ,
,
∴![]() ,
,
当BQ∥DP,则四边形BQDN是平行四边形,
∴BN=QD,
即:![]()
解得:![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,与题意不符,
,与题意不符,
∴不存在这样的t.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】我们可以用![]() 表示
表示![]() 为自变量的函数,如一次函数
为自变量的函数,如一次函数![]() ,可表示
,可表示![]() ,
,![]() ,
,![]() .
.
(1)已知二次函数![]() ;
;
①求证:不论![]() 为何值,此函数图像与
为何值,此函数图像与![]() 轴总有两个交点;
轴总有两个交点;
②若![]() ,是否存在实数
,是否存在实数![]() ,使得当
,使得当![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() ,若存在,求出
,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(2)已知函数![]() ,
,![]() ,若实数
,若实数![]() 、
、![]() 使得
使得![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京第一条地铁线路于1971年1月15日正式开通运营.截至2017年1月,北京地铁共“金山银山,不如绿水青山”.某市不断推进“森林城市”建设,今春种植四类树苗,园林部门从种植的这批树苗中随机抽取了4000棵,将各类树苗的种植棵数绘制成扇形统计图,将各类树苗的成活棵数绘制成条形统计图,经统计松树和杨树的成活率较高,且杨树的成活率为97%,根据图表中的信息解答下列问题:
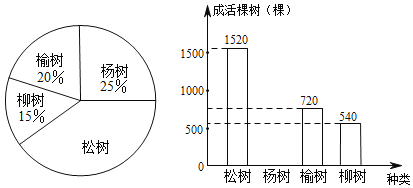
(1)扇形统计图中松树所对的圆心角为 度,并补全条形统计图.
(2)该市今年共种树16万棵,成活了约多少棵?
(3)园林部门决定明年从这四类树苗中选两类种植,请用列表法或树状图求恰好选到成活率较高的两类树苗的概率.(松树、杨树、榆树、柳树分别用A,B,C,D表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
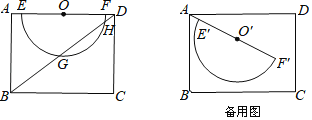
【题目】如图,在矩形ABCD中,AB=6,BC=8,O是AD的中点,以O为圆心在AD的下方作半径为3的半圆O,交AD于E、F.
思考:连接BD,交半圆O于G、H,求GH的长;
探究:将线段AF连带半圆O绕点A顺时针旋转,得到半圆O′,设其直径为E'F′,旋转角为α(0<α<180°).
(1)设F′到AD的距离为m,当m>![]() 时,求α的取值范围;
时,求α的取值范围;
(2)若半圆O′与线段AB、BC相切时,设切点为R,求![]() 的长.
的长.
(sin49°=![]() ,cos41°=
,cos41°=![]() ,tan37°=
,tan37°=![]() ,结果保留π)
,结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() (a,b,c为常数,且
(a,b,c为常数,且![]() )经过点(﹣1,0)和(m,0),且1<m<2,当x<﹣1时,y随着x的增大而减小.下列结论:
)经过点(﹣1,0)和(m,0),且1<m<2,当x<﹣1时,y随着x的增大而减小.下列结论:
①abc>0;
②a+b>0;
③若点A(﹣3,![]() ),点B(3,
),点B(3,![]() )都在抛物线上,则
)都在抛物线上,则![]() <
<![]() ;
;
④![]() ;
;
⑤若若![]() ,则
,则![]() .
.
其中结论错误的是 .(只填写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
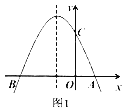
【题目】如图1,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.

(1)求该抛物线的解析式;
(2)在该抛物线的对称轴上是否存在点![]() ,使得
,使得![]() 的周长最小?若存在,求出点
的周长最小?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】桑桑同学利用寒假30天的时间贩卖草莓,某品种草莓的成本为10元/千克,该品种草莓在第![]() 天的销售量与销售单价如下表:
天的销售量与销售单价如下表:
销售量 |
|
销售单价 | 当 |
当 |
(1)请计算第几天该品种草莓的销售单价为25元/千克?
(2)这30天中,该同学第几天获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
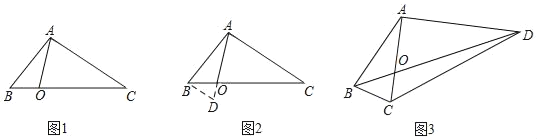
【题目】如图,(1)某学校“智慧方园”数学社团遇到这样一个题目:如图1,在△ABC中,点O在线段BC上,∠BAO=20°,∠OAC=80°,AO=![]() ,BO:CO=1:3,求AB的长.经过社团成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图2),请回答:∠ADB= °,AB= .
,BO:CO=1:3,求AB的长.经过社团成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图2),请回答:∠ADB= °,AB= .
(2)请参考以上思路解决问题:如图3,在四边形ABCD中,对角线AC、BD相交于点O,AC⊥AD,AO=6![]() ,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.
,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴是x=﹣1,且过点(﹣3,0),说法:①abc<0;②2a﹣b=0;③﹣a+c<0;④若(﹣5,y1)、(![]() ,y2)是抛物线上两点,则y1>y2,其中说法正确的有( )个.
,y2)是抛物线上两点,则y1>y2,其中说法正确的有( )个.

A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com