
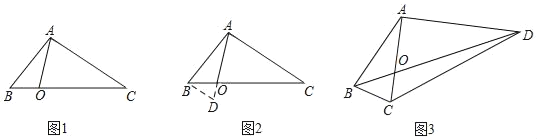
【题目】如图,(1)某学校“智慧方园”数学社团遇到这样一个题目:如图1,在△ABC中,点O在线段BC上,∠BAO=20°,∠OAC=80°,AO=![]() ,BO:CO=1:3,求AB的长.经过社团成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图2),请回答:∠ADB= °,AB= .
,BO:CO=1:3,求AB的长.经过社团成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图2),请回答:∠ADB= °,AB= .
(2)请参考以上思路解决问题:如图3,在四边形ABCD中,对角线AC、BD相交于点O,AC⊥AD,AO=6![]() ,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.
,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.
【答案】(1)80,8![]() ;(2)DC=8
;(2)DC=8![]()
【解析】
(1)根据平行线的性质可得∠ADB=∠OAC=80°,即可证明△BOD∽△COA,可得![]() ,求出AD的长度,再根据角的和差关系得∠ABD=180°﹣∠BAD﹣∠ADB=80°=∠ADB,即可得出AB=AD=8
,求出AD的长度,再根据角的和差关系得∠ABD=180°﹣∠BAD﹣∠ADB=80°=∠ADB,即可得出AB=AD=8![]() .
.
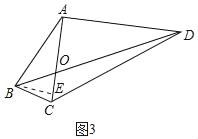
(2)过点B作BE∥AD交AC于点E,通过证明△AOD∽△EOB,可得![]() ,根据线段的比例关系,可得AB=2BE,根据勾股定理求出BE的长度,再根据勾股定理求出DC的长度即可.
,根据线段的比例关系,可得AB=2BE,根据勾股定理求出BE的长度,再根据勾股定理求出DC的长度即可.
解:(1)∵BD∥AC,
∴∠ADB=∠OAC=80°,
∵∠BOD=∠COA,
∴△BOD∽△COA,
∴![]()
∵AO=6![]() ,
,
∴OD=![]() AO=2
AO=2![]() ,
,
∴AD=AO+OD=6![]() +2
+2![]() =8
=8![]() ,
,
∵∠BAD=20°,∠ADB=80°,
∴∠ABD=180°﹣∠BAD﹣∠ADB=80°=∠ADB,
∴AB=AD=8![]() ,
,
故答案为:80,8![]() ;
;
(2)过点B作BE∥AD交AC于点E,如图3所示:
∵AC⊥AD,BE∥AD,
∴∠DAC=∠BEA=90°,
∵∠AOD=∠EOB,
∴△AOD∽△EOB,
∴![]()
∵BO:OD=1:3,
∴![]()
∵AO=6![]() ,
,
∴EO=![]() AO=2
AO=2![]() ,
,
∴AE=AO+EO=6![]() +2
+2![]() =8
=8![]() ,
,
∵∠ABC=∠ACB=75°,
∴∠BAC=30°,AB=AC,
∴AB=2BE,
在Rt△AEB中,BE2+AE2=AB2,即(8![]() )2+BE2=(2BE)2,
)2+BE2=(2BE)2,
解得:BE=8,
∴AB=AC=16,AD=3BE=24,
在Rt△CAD中,AC2+AD2=DC2,即162+242=DC2,
解得:DC=8![]() .
.


科目:初中数学 来源: 题型:
【题目】现种植A、B、C三种树苗一共480棵,安排80名工人一天正好完成,已知每名工人只植一种树苗,且每名工人每天可植A种树苗8棵;或植B种树苗6棵,或植C种树苗5棵.经过统计,在整个过程中,每棵树苗的种植成本如图所示.
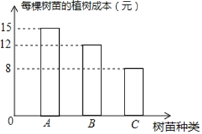
设种植A种树苗的工人为x名,种植B种树苗的工人为y名.
(1)求y与x之间的函数关系式;
(2)若种植的总成本为5600元,从植树工人中随机采访一名工人,求采访到种植C种树苗工人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,![]() ,
,![]() ,动点P从点A出发,在AC上以每秒5cm的速度向点C匀速运动,同时动点Q从点D出发,在DA边上以每秒4cm的速度向点A匀速运动,运动时间为t秒(
,动点P从点A出发,在AC上以每秒5cm的速度向点C匀速运动,同时动点Q从点D出发,在DA边上以每秒4cm的速度向点A匀速运动,运动时间为t秒(![]() ),连接PQ.
),连接PQ.
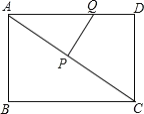
(1)若△APQ与△ADC相似,求t的值;
(2)连结CQ,DP,若![]() ,求t的值;
,求t的值;
(3)连结BQ,PD,请问BQ能和PD平行吗?若能,求出t的值:若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市某幼儿园六一期间举行亲子游戏,主持人请三位家长分别带自己的孩子参加游戏,主持人准备把家长和孩子重新组合完成游戏,A、B、C分别表示三位家长,他们的孩子分别对应的是a、b、c.
(1)若主持人分别从三位家长和三位孩子中各选一人参加游戏,恰好是A、a的概率是多少(直接写出答案)
(2)若主持人先从三位家长中任选两人为一组,再从孩子中任选两人为一组,四人共同参加游戏,恰好是两对家庭成员的概率是多少.(画出树状图或列表)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮利用三张卡片做游戏,卡片上分别写有A,B,B.这些卡片除字母外完全相同,从中随机摸出一张,记下字母后放回,充分洗匀后,再从中摸出一张,如果两次摸到卡片字母相同则小明胜,否则小亮胜,这个游戏对双方公平吗?请说明现由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为
的边长为![]() ,点
,点![]() 与原点重合点
与原点重合点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在
在![]() 轴的负半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形AB′C′D′的位置,B′C′与CD相交于点M,则点M的坐标为__________.
轴的负半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形AB′C′D′的位置,B′C′与CD相交于点M,则点M的坐标为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
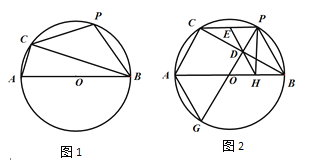
【题目】如图1,以斜边AB为直径作Rt△ABC的外接圆,圆心为O,P为弧BC的中点.
(1)只用直尺和笔作图:在弧ACB另一侧的圆上找一点G,连接PG交BC于点D,使D成为BC中点.并说明你的理由.
(2)在(1)小题图形基础上,在DG上取一点K,使DK=DP,连接CK、BK,判断四边形PBKC的形状,并证明你的结论.
(3)如题图2,取CP的中点E,连接ED并延长ED交AB于点H,连接PH,求证:当∠CAB=60°时,H为AB四等分点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,老师提出了这样一个问题:如图,己知![]() .求作:过
.求作:过![]() 三点的圆.
三点的圆.
小芸是这样思考的:圆心确定一个圈的位置,半径确定一个圆的大小要作同时经过几个定点的圆,就是要先找到一个点,使得这个点到这几个定点的距离都相等.这样既定了圆心,又定了半径,就能画出满足条件的圆了.
小智听了小芸的分析后,按照这个思路很快就画出了一个过![]() 三点的圆.
三点的圆.
请你在答题纸上而出这个圆,并写出作图的主要依据,

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com