【题目】如图是二次函数y＝ax2+bx+c图象的一部分，其对称轴是x＝﹣1，且过点(﹣3，0)，说法：①abc＜0；②2a﹣b＝0；③﹣a+c＜0；④若(﹣5，y1)、(
，y2)是抛物线上两点，则y1＞y2，其中说法正确的有( )个．
A.1B.2C.3D.4
【答案】D
【解析】
由抛物线开口方向得到a＞0，根据抛物线的对称轴得b＝2a＞0，则2a﹣b＝0，则可对②进行判断；根据抛物线与y轴的交点在x轴下方得到c＜0，则abc＜0，于是可对①进行判断；由于x＝﹣1时，y＜0，则得到a﹣2a+c＜0，则可对③进行判断；通过点(﹣5，y1)和点(
，y2)离对称轴的远近对④进行判断．
解：∵抛物线开口向上，
∴a＞0，
∵抛物线对称轴为直线x＝﹣
＝﹣1，
∴b＝2a＞0，则2a﹣b＝0，所以②正确；
∵抛物线与y轴的交点在x轴下方，
∴c＜0，
∴abc＜0，所以①正确；
∵x＝﹣1时，y＝a﹣b+c＜0，
∵b＝2a，
∴a﹣2a+c＜0，即﹣a+c＜0，所以③正确；
∵点(﹣5，y1)离对称轴要比点(，y2)离对称轴要远，
∴y1＞y2，所以④正确．
故答案为D．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，矩形ABCD中，
，
，动点P从点A出发，在AC上以每秒5cm的速度向点C匀速运动，同时动点Q从点D出发，在DA边上以每秒4cm的速度向点A匀速运动，运动时间为t秒（
），连接PQ.
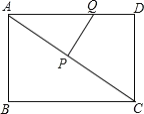
（1）若△APQ与△ADC相似，求t的值；
（2）连结CQ，DP，若
，求t的值；
（3）连结BQ，PD，请问BQ能和PD平行吗？若能，求出t的值：若不能，说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
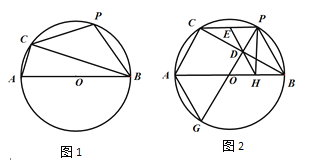
【题目】如图1，以斜边AB为直径作Rt△ABC的外接圆，圆心为O，P为弧BC的中点．
（1）只用直尺和笔作图：在弧ACB另一侧的圆上找一点G，连接PG交BC于点D，使D成为BC中点．并说明你的理由．
（2）在（1）小题图形基础上，在DG上取一点K，使DK＝DP，连接CK、BK，判断四边形PBKC的形状，并证明你的结论．
（3）如题图2，取CP的中点E，连接ED并延长ED交AB于点H，连接PH，求证：当∠CAB＝60°时，H为AB四等分点．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（2016广东省深圳市）荔枝是深圳的特色水果，小明的妈妈先购买了2千克桂味和3千克糯米糍，共花费90元；后又购买了1千克桂味和2千克糯米糍，共花费55元．（每次两种荔枝的售价都不变）
（1）求桂味和糯米糍的售价分别是每千克多少元；
（2）如果还需购买两种荔枝共12千克，要求糯米糍的数量不少于桂味数量的2倍，请设计一种购买方案，使所需总费用最低．
查看答案和解析>>
科目：初中数学 来源： 题型：
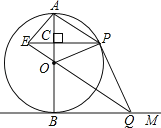
【题目】如图，AB是⊙O的直径，BM切⊙O于点B，点P是⊙O上的一个动点(点P不与A，B两点重合)，连接AP，过点O作OQ∥AP交BM于点Q，过点P作PE⊥AB于点C，交QO的延长线于点E，连接PQ，OP．
(1)求证：△BOQ≌△POQ；
(2)若直径AB的长为12．
①当PE＝ 时，四边形BOPQ为正方形；
②当PE＝ 时，四边形AEOP为菱形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线y=(x-m)2-(x-m)，其中m是常数．
（1）求证：不论m为何值，该抛物线与x轴一定有两个公共点．
（2）若该抛物线的对称轴为直线
，求该抛物线的函数表达式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】数学课上，老师提出了这样一个问题：如图，己知
.求作：过
三点的圆．
小芸是这样思考的：圆心确定一个圈的位置，半径确定一个圆的大小要作同时经过几个定点的圆，就是要先找到一个点，使得这个点到这几个定点的距离都相等．这样既定了圆心，又定了半径，就能画出满足条件的圆了．
小智听了小芸的分析后，按照这个思路很快就画出了一个过三点的圆．
请你在答题纸上而出这个圆，并写出作图的主要依据，
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
