练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

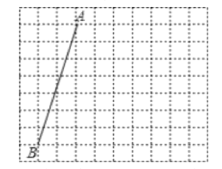
    【题目】如图,方格纸中每个小正方形的边长均为1.线段AB的两个端点在小正方形的顶点上。

    (1)在图中画一个以AB为腰的等腰三角形△ABC点C在小正方形的顶点上,且tan∠B=3；

    (2)在图中画一个以AB为底的等腰三角形△ABD点D在小正方形的项点上,且△ABD是锐角三角形。连接CD,请直接写出线段CD的长。

    【答案】（1）详见解析；（2）图详见解析，.

    【解析】

    (1)因为AB为腰、tan∠B=3的等腰△ABC,由此即可画出图形

    (2)因为AB为底、△ABD是锐角三角形的等腰△ABC,所以点C在线段AB的垂直平分线上,由此即可画出图形,利用勾股定理计算CD的长

    (1)如图所示:△ABC即为所求

    (2)如图所示:△ABD即为所求

    CD=

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】每年5月的第二个星期日即为母亲节，“父母恩深重，恩怜无歇时”，许多市民喜欢在母亲节为母亲送鲜花，感恩母亲，祝福母亲. 节日前夕，某花店采购了一批鲜花礼盒，成本价为30元每件，分析上一年母亲节的鲜花礼盒销售情况，得到了如下数据，同时发现每天的销售量（件）是销售单价（元/件）的一次函数.

    销售单价 (元/件)

    …

    30

    40

    50

    60

    …

    每天销售量 (件)

    …

    350

    300

    250

    200

    …

    （1）求出与的函数关系；

    （2）物价局要求,销售该鲜花礼盒获得的利润不得高于100﹪：

    ①当销售单价取何值时,该花店销售鲜花礼盒每天获得的利润为5000元?(利润=销售总价-成本价)；

    ②试确定销售单价取何值时，花店销该鲜花礼盒每天获得的利润（元）最大？并求出花店销该鲜花礼盒每天获得的最大利润.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线与轴交于，两点，与轴交于点，抛物线的对称轴与轴交于点，顶点坐标为.

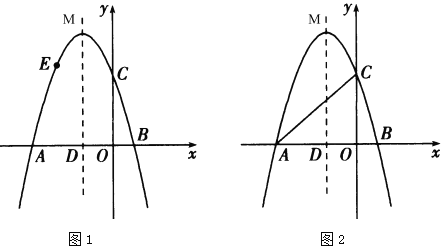
    （1）求抛物线的表达式和顶点的坐标；

    （2）如图1，点为抛物线上一点，点不与点重合，当时，过点作轴，交抛物线的对称轴于点，作轴于点H，得到矩形，求矩形的周长的最大值；

    （3）如图2，点为抛物线对称轴上一点，是否存在点，使以点、、为顶点的三角形是直角三角形？若存在，求出点的坐标；若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

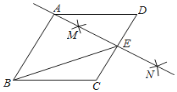
    【题目】如图，在菱形中，，按以下步骤作图：①分别以点和点为圆心，为圆心，大于号的长为半径面狐，两弧交于点，：②做直线，且恰好经过点，与交于点，连接，则的值为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，②分别是某款篮球架的实物图和示意图，已知支架AB的长为2.3m，支架AB与地面的夹角∠BAC＝70°，BE的长为1.5m，篮板部支架BD与水平支架BE的夹角为46°，BC、DE垂直于地面，求篮板顶端D到地面的距离．(结果保留一位小数，参考数据：sin70°≈0.94，cos70°≈0.34，tan70°≈2.75，sin46°≈0.72，cos46°≈0.69，tan46°≈1.04)

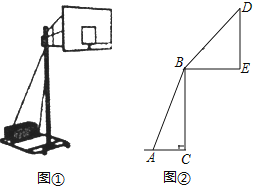
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】关于的一元二次方程，给出下列说法：①若，则方程必有两个实数根；②若，则方程必有两个实数根；③若，则方程有两个不相等的实数根；④若，则方程一定没有实数根．其中说法正确的序号是( )

    A. ①②③B. ①②④

    C. ①③④D. ②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

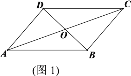
    【题目】我们把有两边对应相等，且夹角互补(不相等)的两个三角形叫做“互补三角形”，如图1，□ABCD中，△AOB和△BOC是“互补三角形”.

    (1)写出图1中另外一组“互补三角形”_______；

    (2)在图2中，用尺规作出一个△EFH，使得△EFH和△EFG为“互补三角形”，且△EFH和△EFG在EF同侧，并证明这一组“互补三角形”的面积相等.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙二人从学校出发去新华书店看书，甲步行一段时间后，乙骑自行车沿相同路线行进两人均匀速前行，他们之间的距离s(米)与甲出发时间t(分)之间的函数关系如图所示．下列说法错误的是( )

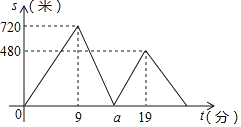
    A. 乙的速度是甲速度的2.5倍

    B. a＝15

    C. 学校到新华书店共3800米

    D. 甲第25分钟到达新华书店

    查看答案和解析>>

    科目：初中数学 来源： 题型：

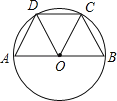
    【题目】如图，C、D为半圆上三等分点，则下列说法：①==；②∠AOD＝∠DOC＝∠BOC；③AD＝CD＝OC；④△AOD沿OD翻折与△COD重合．正确的有（ ）

    A. 4个B. 3个C. 2个D. 1个

    查看答案和解析>>

    同步练习册答案