
【题目】若将一幅三角板按如图所示的方式放置,则下列结论中不正确的是( )
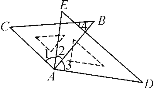
A. ∠1=∠3 B. 如果∠2=30°,则有AC∥DE
C. 如果∠2=30°,则有BC∥AD D. 如果∠2=30°,必有∠4=∠C
科目:初中数学 来源: 题型:
【题目】某校学生在电脑培训前后各参加了一次水平相同的考试,考分都以同一标准划分成“不合格”、“合格”、“优秀”三个等级.为了了解电脑培训的效果,随机抽取其中32名学生两次考试考分等级制成统计图(如图),试回答下列问题: 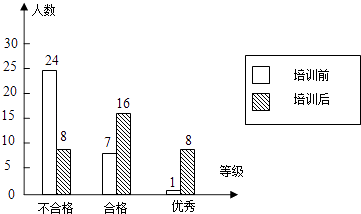
(1)这32名学生经过培训,考分等级“不合格”的百分比由下降到;
(2)估计该校640名学生,培训后考分等级为“合格”与“优秀”的学生共有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在三角形ABC中,点E,F分别为线段AB,AC上任意两点,EG交BC于点G,交AC的延长线于点H,∠1+∠AFE=180°.
(1)证明:BC∥EF;
(2)如图②,若∠2=∠3,∠BEG=∠EDF,证明:DF平分∠AFE.
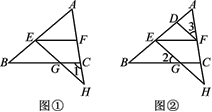
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尤秀同学遇到了这样一个问题:如图1所示,已知AF,BE是△ABC的中线,且AF⊥BE,垂足为P,设BC=a,AC=b,AB=c.
求证:a2+b2=5c2
该同学仔细分析后,得到如下解题思路:
先连接EF,利用EF为△ABC的中位线得到△EPF∽△BPA,故 ![]() ,设PF=m,PE=n,用m,n把PA,PB分别表示出来,再在Rt△APE,Rt△BPF中利用勾股定理计算,消去m,n即可得证
,设PF=m,PE=n,用m,n把PA,PB分别表示出来,再在Rt△APE,Rt△BPF中利用勾股定理计算,消去m,n即可得证
(1)请你根据以上解题思路帮尤秀同学写出证明过程.
(2)利用题中的结论,解答下列问题:在边长为3的菱形ABCD中,O为对角线AC,BD的交点,E,F分别为线段AO,DO的中点,连接BE,CF并延长交于点M,BM,CM分别交AD于点G,H,如图2所示,求MG2+MH2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.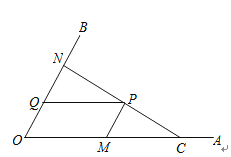
(1)若∠AOB=60°,OM=4,OQ=1,求证:CN⊥OB
(2)当点N在边OB上运动时,四边形OMPQ始终保持为菱形.
①问:![]() ﹣
﹣![]() 的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由.
的值是否发生变化?如果变化,求出其取值范围;如果不变,请说明理由.
②设菱形OMPQ的面积为S1 , △NOC的面积为S2 , 求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人都去同一家超市购买大米各两次,甲每次购买50千克的大米,乙每次购买50元的大米,这两人第一次购买大米时售价为每千克m元,第二次购买大米时售价为每千克n元(m≠n),若规定谁两次购买大米的平均单价低,谁的购买方式就合算,则下列观点正确的是( )
A. 甲的购买方式合算 B. 乙的购买方式合算
C. 甲、乙的购买方式同样合算 D. 不能判断谁的购买方式合算
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙0的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD.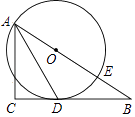
(1)求证:AD平分∠BAC;
(2)若AC=8,tan∠DAC= ![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线OA的方向是北偏东20,射线OB的方向是北偏西40,OD是OB的反向延长线,OC是∠AOD的平分线。
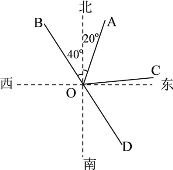
(1)求∠BOC的度数;
(2)求出射线OC的方向。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com