
 如图,已知点A1,A2,…,An均在直线y=x-1上,点B1,B2,…,Bn均在双曲线y=-$\frac{1}{x}$上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2015=2.
如图,已知点A1,A2,…,An均在直线y=x-1上,点B1,B2,…,Bn均在双曲线y=-$\frac{1}{x}$上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2015=2. 分析 首先根据a1=-1,求出a2=2,a3=$\frac{1}{2}$,a4=-1,a5=2,…,所以a1,a2,a3,a4,a5,…,每3个数一个循环,分别是-1、2、$\frac{1}{2}$;然后用2015除以3,根据商和余数的情况,判断出a2015是第几个循环的第几个数,进而求出它的值是多少即可.
解答 解:∵a1=-1,
∴B1的坐标是(-1,1),
∴A2的坐标是(2,1),
即a2=2,
∵a2=2,
∴B2的坐标是(2,-$\frac{1}{2}$),
∴A3的坐标是($\frac{1}{2}$,-$\frac{1}{2}$),
即a3=$\frac{1}{2}$,
∵a3=$\frac{1}{2}$,
∴B3的坐标是($\frac{1}{2}$,-2),
∴A4的坐标是(-1,-2),
即a4=-1,
∵a4=-1,
∴B4的坐标是(-1,1),
∴A5的坐标是(2,1),
即a5=2,
…,
∴a1,a2,a3,a4,a5,…,每3个数一个循环,分别是-1、2、$\frac{1}{2}$,
∵2015÷3=671…2,
∴a2015是第672个循环的第2个数,
∴a2015=2.
故答案为:2.
点评 (1)此题主要考查了反比例函数图象上点的坐标的特征,要熟练掌握,解答此题的关键是要明确:①图象上的点(x,y)的横纵坐标的积是定值k,即xy=k;②双曲线是关于原点对称的,两个分支上的点也是关于原点对称;③在xk图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
(2)此题还考查了一次函数图象上的点的坐标特征,要熟练掌握,解答此题的关键是要明确:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-$\frac{b}{k}$,0);与y轴的交点坐标是(0,b).直线上任意一点的坐标都满足函数关系式y=kx+b.


 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:解答题
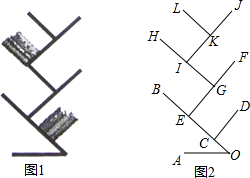 图1是小明利用废弃的钢条焊接成的创意书架,现将其结构简化成图2所示的图形,制作过程为:首先将两根钢条OA和OB焊接成∠AOB=45°,OB=70cm,BC=EF=HG=IJ=60cm,焊接点E、G、I分别为BC、EF、HG的中点,钢条KL、CD的长均为30cm,所有在点C,E,G,I,K焊接处的相邻两根钢条互相垂直.
图1是小明利用废弃的钢条焊接成的创意书架,现将其结构简化成图2所示的图形,制作过程为:首先将两根钢条OA和OB焊接成∠AOB=45°,OB=70cm,BC=EF=HG=IJ=60cm,焊接点E、G、I分别为BC、EF、HG的中点,钢条KL、CD的长均为30cm,所有在点C,E,G,I,K焊接处的相邻两根钢条互相垂直.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图是一个半圆形桥洞的截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD∥AB,且CD=24cm,OE⊥CD于点E,现测得sin∠DOE=$\frac{12}{13}$,则水深是5m.
如图是一个半圆形桥洞的截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD∥AB,且CD=24cm,OE⊥CD于点E,现测得sin∠DOE=$\frac{12}{13}$,则水深是5m.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
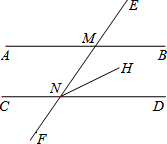 如图,已知直线AB∥CD,且直线EF分别交AB、CD于M、N两点,NH是∠MND的角平分线.若∠AMN=56°,则∠MNH的度数是( )
如图,已知直线AB∥CD,且直线EF分别交AB、CD于M、N两点,NH是∠MND的角平分线.若∠AMN=56°,则∠MNH的度数是( )| A. | 28° | B. | 30° | C. | 34° | D. | 56° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
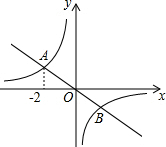 如图,双曲线y=$\frac{k}{x}$与直线y=-$\frac{1}{2}$x交于A、B两点,且A(-2,m),则点B的坐标是( )
如图,双曲线y=$\frac{k}{x}$与直线y=-$\frac{1}{2}$x交于A、B两点,且A(-2,m),则点B的坐标是( )| A. | (2,-1) | B. | (1,-2) | C. | ($\frac{1}{2}$,-1) | D. | (-1,$\frac{1}{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 摸出的2个球都是白球 | B. | 摸出的2个球有一个是白球 | ||
| C. | 摸出的2个球都是黑球 | D. | 摸出的2个球有一个黑球 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com