
分析 (1)设每件衬衫应降价x元,根据题意得:(40-x)(30+3x)=1872,求出x的值,再根据要使在价格方面具有较强的竟争力,即可求出答案;
(2)设每天要赢利y元,根据①的解答结果可得;y=-(x-15)2+1875,再求出最大值即可.
解答 解:(1)设每件衬衫应降价x元,根据题意得:
(40-x)(30+3x)=1872
解得:x1=14,x2=16,
∵要使在价格方面具有较强的竟争力,
∴x=16.
答:每件衬衫应降价16元;
(2)设每天要赢利y元,根据(1)的解答结果可得:
y=(40-x)(30+3x)=-3x2+90x+1200=-(x-15)2+1875,
故当每件衬衫降价15元时,赢利最多,最多的赢利为1875元.
点评 本题考查了二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题,关键是根据题意求出函数关系式.


科目:初中数学 来源: 题型:填空题
 如图,已知点A1,A2,…,An均在直线y=x-1上,点B1,B2,…,Bn均在双曲线y=-$\frac{1}{x}$上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2015=2.
如图,已知点A1,A2,…,An均在直线y=x-1上,点B1,B2,…,Bn均在双曲线y=-$\frac{1}{x}$上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2015=2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{120}{x-5}$=$\frac{100}{x}$ | B. | $\frac{120}{x}$=$\frac{100}{x-5}$ | C. | $\frac{120}{x+5}$=$\frac{100}{x}$ | D. | $\frac{120}{x}$=$\frac{100}{x+5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
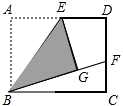 (1)如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=1,FD=2,则BC的长为2$\sqrt{6}$.
(1)如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=1,FD=2,则BC的长为2$\sqrt{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com