
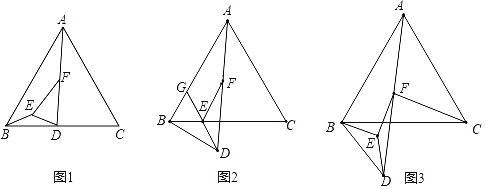
【题目】如图1,已知△ABC是边长为8的等边三角形,∠EBD=30°,BE=DE,连接AD,点F为AD的中点,连接EF.将△BDE绕点B顺时针旋转.
(1)如图2,当点E位于BC边上时,延长DE交AB于点G.
①求证:BG=DE;
②若EF=3,求BE的长;
(2)如图3,连接CF,在旋转过程中试探究线段CF与EF之间满足的数量关系,并说明理由.
【答案】(1)①见解析;②2;(2)EC=![]() EF,EC⊥EF,见解析
EF,EC⊥EF,见解析
【解析】
(1)①想办法证明△BEG是等边三角形即可解决问题;②利用三角形的中位线定理求出AG,再求出BG即可解决问题.
(2)结论:EC=![]() EF,EC⊥EF.延长DF交CA的延长线于M,延长FE到K,使得EK=EF,连接AK,CK,CF,在FM上截取FN=DF,连接BN.证明图中,红色三角形全等,推出△CFK是等边三角形即可解决问题.
EF,EC⊥EF.延长DF交CA的延长线于M,延长FE到K,使得EK=EF,连接AK,CK,CF,在FM上截取FN=DF,连接BN.证明图中,红色三角形全等,推出△CFK是等边三角形即可解决问题.
(1)①证明:如图2中,
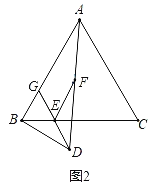
∵△ABC是等边三角形,
∴∠ABC=60°,
∵EB=ED,
∴∠EBD=∠EDB=30°,
∴∠GBD=∠ABC+∠EBD=90°,
∴∠BGD=60°,
∴△BEG是等边三角形,
∴BG=BE,
∴BG=ED.
②解:由①可知,BG=GE=BE=DE,
又∵AF=DF,
∴AG=2EF=6,
∵AB=8,
∴BG=AB﹣AG=8﹣6=2,
∴BE=BG=2.
(2)结论:EC=![]() EF,EC⊥EF.
EF,EC⊥EF.
理由:如图2中,延长DF交CA的延长线于M,延长FE到K,使得EK=EF,连接AK,CK,CF,在FM上截取FN=DF,连接BN.

∵FB=FD=FN,
∴∠DBN=90°,
∵∠DBF=30°,
∴∠FBN=60°,
∴△FBN是等边三角形,
∴BN=BF,
∵∠ABC=∠NBF=60°,
∴∠ABN=∠CBF,
∵AB=BC,
∴△ABN≌△CBF(SAS),
∴AN=CF,
∵FN=DF,AE=ED,
∴EF∥AN,AN=2EF,
∵2EF=FK,
∴AN=FK,AN∥FK,
∴四边形ANFK是平行四边形,
∴AK∥DM,AK=FN=BN,
∴∠CAK=∠M,
∵∠AOM=∠BON,∠OAM=∠BNO=120°,
∴∠M=∠OBN,
∴∠ABN=∠CAK,
∵AB=AC,
∴△ABN≌△CAK(SAS),
∴AN=CK,
∴CF=CK=FK,
∴△CFK是等边三角形,∠CFE=60°
∵2EF=FK,
∴CE⊥FK,
∵∠EFC=60°,
∴tan∠CFE=![]() =
=![]() ,
,
∴EC=![]() EF,EC⊥EF.
EF,EC⊥EF.


科目:初中数学 来源: 题型:
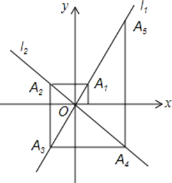
【题目】在平面角坐标系中,函数y=2x和y=-x的图像分别为直线l1、l2,过点(1,0)作x轴的垂线交l2于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…,依次进行下去,则点A2020的坐标为_______________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校共抽取50名同学参加学校举办的“预防新冠肺炎”知识测验,所得成绩分别记作60分、70分、80分、90分、100分,并将统计结果绘制成不完整的扇形统计图(如图).
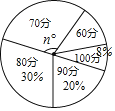
(1)若n=108,则成绩为60分的人数为 ;
(2)若从这50位同学中,随机抽取一人,求抽到同学的分数不低于90分的概率;
(3)若成绩的唯一众数为80分,求这个班平均成绩的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】崇州(古称蜀州),老子思想创立发扬地,崇州市历史悠久,汉代称蜀川,唐代称蜀州,其建制历史长达4300年,公元316年设立县制,1994年撤县设市.崇州市全市幅员面积1090平方公里,呈“四山一水五分田”格局,是距离成都天府广场最近的郊区区域,是四川省首批命名的历史悠久名城,辖6个街道办事处,9个镇,户籍人口66.48万(其中城镇人口31.6万),常住人口75万,用科学记数法表示75万为( )
A.7.5×104B.75×104C.0.75×106D.7.5×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径.∠ACB的平分线CD交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.
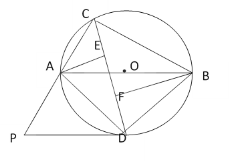
(1)求证:DP∥AB;
(2)试猜想线段AE、EF、BF之间的数量关系,并加以证明;
(3)若AC=6,BC=8,求线段PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
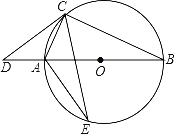
【题目】如图,AB是⊙O的直径,点C、E位于⊙O上AB两侧.在BA的延长线上取点D,使∠ACD=∠B.
(1)求证:DC是⊙O的切线;
(2)当BC=EC时,求证:AC2=AEAD;
(3)在(2)的条件下,若BC=4![]() ,AD:AE=5:9,求⊙O的半径.
,AD:AE=5:9,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
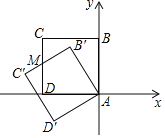
【题目】如图,正方形ABCD的边长为1,点A与原点重合,点B在y轴的正半轴上,点D在x轴的负半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形AB'C′D′的位置,B'C′与CD相交于点M,则点M的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中选出一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.
类别 |
|
|
|
|
|
类型 | 新闻 | 体育 | 动画 | 娱乐 | 戏曲 |
人数 | 11 | 20 | 40 |
| 4 |
请你根据以上信息,回答下列问题:
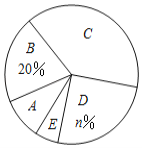
(1)统计表中![]() 的值为_______,统计图中
的值为_______,统计图中![]() 的值为______,
的值为______,![]() 类对应扇形的圆心角为_____度;
类对应扇形的圆心角为_____度;
(2)该校共有1500名学生,根据调查结果,估计该校最喜爱体育节目的学生人数;
(3)样本数据中最喜爱戏曲节目的有4人,其中仅有1名男生.从这4人中任选2名同学去观赏戏曲表演,请用树状图或列表求所选2名同学中有男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ABC内接于⊙O,AB=AC,
ABC内接于⊙O,AB=AC,![]() .过点A作AD//BC,与
.过点A作AD//BC,与![]() 的平分线交于点D,BD与AC交于点E,与⊙O交于点F.
的平分线交于点D,BD与AC交于点E,与⊙O交于点F.
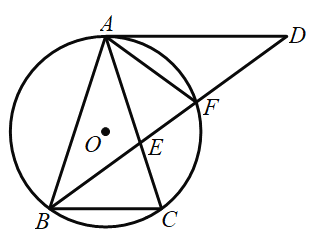
(1)求证:AD是⊙O的切线
(2)求证:![]()
(3)若BC=2,求![]() 的值
的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com