【题目】甲、乙两人都从
出发经
地去
地，乙比甲晚出发1分钟，两人同时到达地，甲在地停留1分钟，乙在地停留2分钟，他们行走的路程
（米）与甲行走的时间
（分钟）之间的函数关系如图所示，则下列说法中正确的个数有（ ）
①甲到地前的速度为
②乙从地出发后的速度为
③、两地间的路程为
④甲乙在行驶途中再次相遇时距离地
A.1个B.2个C.3个D.4个
【答案】C
【解析】
①②③直接利用图中信息即可解决问题，求出到B地后的函数关系式，利用方程组求交点坐标即可判定④的正确性．
解：由图象可知：甲到B地前的速度为400÷4=100米/分钟，故①正确，
乙从B地出发后的速度为600÷2=300米/分钟，故②错误，
由图象可知，A、C两地间的路程为1000米，故③正确，
设甲到B地后的函数关系为y=kx+b，则有
，
解得
，
∴y=150x-350，
设乙到B地后的函数关系为y=mx+n，则有
，
解得
，
∴y=300x-1400，
由
解得
，
∴甲乙再次相遇时距离A地700米，
∵1000-700=300，
∴甲乙再次相遇时距离C地300米，故④正确，
故选：C．
科目：初中数学 来源： 题型：
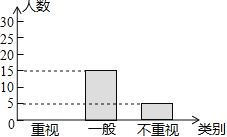
【题目】某教研机构为了了解初中生课外阅读名著的现状，随机抽取了某校50名初中生进行调查，依据相关数据绘制成了以下不完整的统计图，请根据图中信息解答下列问题：
类别 | 重视 | 一般 | 不重视 |
人数 | a | 15 | b |
（1）求表格中a，b的值；
（2）请补全统计图；
（3）若某校共有初中生2000名，请估计该校“重视课外阅读名著”的初中生人数．
查看答案和解析>>
科目：初中数学 来源： 题型：
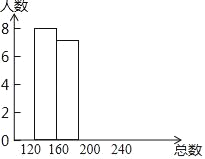
【题目】为培养学生庭好的学习习惯，某校九年级年级组举行“整理错题集“的征集展示活动，并随机对部分学生三年“整理题集”中收集的错题数x进行了抽样调查，根据收集的数据绘制了下面不完整的统计图表．
分组 | 频数 | 频率 |
第一组（0≤x＜120） | 3 | 0.15 |
第二组（120≤x＜160） | 8 | a |
第三组（160≤x＜200） | 7 | 0.35 |
第四组（200≤x＜240） | b | 0.1 |
请你根据图表中的信息完成下列问题：
（1）频数分布表中a＝ ，b＝ ，并将统计图补充完整；
（2）如果该校九年级共有学生360人，估计整理的错题数在160或160题以上的学生有多少人？
（3）已知第一组中有两个是甲班学生，第四组中有一个是甲班学生，老师随机从这两个组中各选一名学生谈整理错题的体会，则所选两人正好都是甲班学生的概率是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为推进生态文明建设，甲、乙两工程队同时为崂山区的两条绿化带铺设草坪．两队所铺设草坪的面积
（米）与施工时间
（时）之间关系的近似可以用此图象描述．请结合图象解答下列问题：
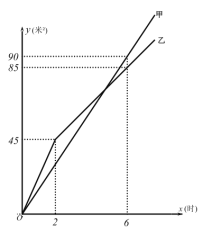
（1）从工作2小时开始，施工方从乙队抽调两人对草坪进行灌溉，乙队速度有所降低，求乙队在工作2小时后与的函数关系式；
（2）求乙队降速后，何时铺设草坪面积为甲队的
？
（3）乙队降速后，甲乙两队铺设草坪速度之比为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】六
一前夕，某幼儿园园长到厂家选购A、B两种品牌的儿童服装，每套A品牌服装进价比B品牌服装每套进价多25元，用2000元购进A种服装数量是用750元购进B种服装数量的2倍．
求A、B两种品牌服装每套进价分别为多少元？
该服装A品牌每套售价为130元，B品牌每套售价为95元，服装店老板决定，购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套，两种服装全部售出后，可使总的获利超过1200元，则最少购进A品牌的服装多少套？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】抛物线y=ax2+bx+5a与x轴有两个交点是点A和点B（点B在点A左边）且抛物线交y轴于负半轴，a与b异号．则下列说法中正确的一项是（ ）
A.若抛物线上仅有一点C(m，m)则a的取值范围为
B.方程ax2+bx+3a=0必有两个不相等的实数根
C.当b=6a时，点B(-1，0)，点A(5，0)
D.a与b满足大小关系为
查看答案和解析>>
科目：初中数学 来源： 题型：
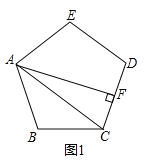
【题目】我们学过正多边形及其性质，了解了正多边形各边相等、各内角相等、具有轴对称性和旋转不变．．．．下面我们继续探究正五边形相关线段及角的关系：
如图1，正五边形
中，
连接
，并作
，则
度；
连接
交于点
，求证：四边形
是菱形；
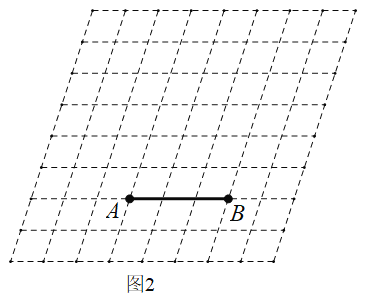
如图2，是一个斜网格图
， 每个小菱形的较小内角是
，请利用一把角尺(只能画直角和直线，不能度量，可以用三角板替代)在网格图中画出以
为一边的正五边形(保留作图痕迹)．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】朝阳公司以10元/千克的价格收购一批产品进行销售，经过市场调查发现：日销售量y（千克）与销售价格x（元/千克）之间是一次函数关系，当销售价格x是10元/千克时，日销售量y是300千克，当销售价格x是20元/千克时，日销售量y是150千克．
（1）求y与x之间的函数表达式；
（2）朝阳公司应该如何确定这批产品的销售价格，才能使日销售利润W1元最大？
（3）若朝阳公司每销售1千克这种产品需支出a元（a＞0）的相关费用，当20≤x≤25时，公司的日获利W2元的最大值为1215元，求a的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
