
【题目】如图,在△ABC中,AD平分∠BAC,过B作BE⊥AD于E,过E作EF∥AC交AB于F,则下列结论:(1)AF=FE,(2)FE=FB,(3)FE=BE,(4)AF=BF,(5)BE =BF,成立的有( )

A.1 个B.2 个C.3个D.4个
【答案】C
【解析】
根据角平分线的定义可得∠1=∠2,根据两直线平行,内错角相等可得∠2=∠3,从而得到∠1=∠3,再根据等角对等边可得AF=FE,根据垂直定义和直角三角形两锐角互余可得∠3+∠5=90°,∠1+∠4=90°,从而求出∠4=∠5,再根据等角对等边可得FB=FE,对各结论逐一判断即可.
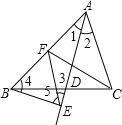
解:如图,∵AD平分∠BAC,
∴∠1=∠2,
∵EF∥AC,
∴∠2=∠3,
∴∠1=∠3,
∴AF=FE,故(1)正确;
∵BE⊥AD,
∴∠3+∠5=90°,∠1+∠4=90°,
∴∠4=∠5,
∴FE=FB,故(2)正确;
∴AF=BF=FE,故(4)正确,
∵无法判断出△BEF是等边三角形,
∴FE=BE与BE=BF不一定成立,故(3)(5)错误;
综上所述,正确的是(1)(2)(4)共3个.
故选:C.


科目:初中数学 来源: 题型:
【题目】在一个袋子中装有大小相同的![]() 个小球,其中
个小球,其中![]() 个蓝色,
个蓝色,![]() 个红色.
个红色.
![]() 从袋中随机摸出
从袋中随机摸出![]() 个,求摸到的是蓝色小球的概率;
个,求摸到的是蓝色小球的概率;
![]() 从袋中随机摸出
从袋中随机摸出![]() 个,用列表法或树状图法求摸到的都是红色小球的概率;
个,用列表法或树状图法求摸到的都是红色小球的概率;
![]() 在这个袋中加入
在这个袋中加入![]() 个红色小球,进行如下试验:随机摸出
个红色小球,进行如下试验:随机摸出![]() 个,然后放回,多次重复这个试验,通过大量重复试验后发现,摸到红色小球的频率稳定在
个,然后放回,多次重复这个试验,通过大量重复试验后发现,摸到红色小球的频率稳定在![]() ,则可以推算出
,则可以推算出![]() 的值大约是多少?
的值大约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料
在因式分解中,把多项式中某些部分看作一个整体,用一个新的字母代替(即换元),不仅可以简化要分解的多项式的结构,而且能使式子的特点更加明显,使于观察如何进行因式分解我们把这种因式分解的方法称为“换元 法”.下面是小涵同学用换元法对多项式(x+4x+1)(x+4x+7)+9 进行因式分解的过程.
解:设 x+4x=y
原式=(y+1)(y+7)+9 (第一步)
=y+8y+16 (第二步)
=(y+4) (第三步)
=(x+4x+4) (第四步)
请根据上述材料回答下列问题:
(1)小涵同学的解法中,第二步到第三步运用了因式分解的 .
A.提取公因式法 B.平方差公式法 C.完全平方公式法
(2)老师说,小涵同学因式分解的结果不彻底,请你写出该因式分解的最后结果: .
(3)请你用换元法对多项式(x-2x)(x-2x+2)+1 进行因式分解
(4)当 x= 时,多项式(x-2x)(x-2x+2)-1 存在最 值(填“大”或“小”).请你求出这 个最值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,AB=8cm,BC=6cm.动点P、Q分别从点A、B同时开始移动,点P的速度为1 cm/秒,点Q的速度为2 cm/秒,点Q移动到点C后停止,点P也随之停止运动下列时间瞬间中,能使△PBQ的面积为15cm 的是( )

A. 2秒钟 B. 3秒钟 C. 4秒钟 D. 5秒钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=5cm,BC=3cm,AC=4cm,若动点P从点C开始,按照C→A→B的路径运动,且运动速度为每秒2cm,设出发的时间为t秒.
(1)请判断△ABC的形状,说明理由
(2)当t为何值时,△BCP是以BC为腰的等腰三角形,求出t的值
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒1cm,若P、Q两点同时出发, 当P、Q中有一点到达终点时,另一点也停止运动,当t为何值时,P、Q两点之间的距离为![]() ,直接写出t的值.
,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P的坐标为(-3,4),作出点P关于x轴对称的点P1,称为第1次变换;再作出点P1关于y轴对称的点P2,称为第2次变换;再作点P2关于x轴对称的点P3,称为第3次变换,…,依次类推,则第2019次变换得到的点P2019的坐标为 ____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列一段文字,再回答后面的问题.
已知在平面内两点P1(x1,y1),P2(x2,y2),这两点间的距离P1P2=![]() ,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.
,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.
(1)已知A(3,3),B(﹣2,﹣1),试求A,B两点间的距离;
(2)已知A,B在平行于y轴的直线上,点A的纵坐标为7,点B的纵坐标为﹣2,试求A,B两点间的距离;
(3)已知一个三角形各顶点坐标为A(0,5),B(﹣3,2),C(3,2),你能判断此三角形的形状吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽和小华想利用摸球游戏决定谁去参加市里举办的书法比赛,游戏规则是:在一个不透明的袋子里装有除数字外完全相同的4个小球,上面分别标有数字2,3,4,5.一人先从袋中随机摸出一个小球,另一人再从袋中剩下的3个小球中随机摸出一个小球.若摸出的两个小球上的数字和为偶数,则小丽去参赛;否则小华去参赛.
(1)用列表法或画树状图法,求小丽参赛的概率.
(2)你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,菱形
,菱形![]() 对角线
对角线![]() 、
、![]() 的交点
的交点![]() 是四边形
是四边形![]() 对角线
对角线![]() 的中点,四个顶点
的中点,四个顶点![]() 、
、![]() 、
、![]() 、
、![]() 分别在四边形
分别在四边形![]() 的边
的边![]() 、
、![]() 、
、![]() 、
、![]() 上.
上.
![]() 求证:四边形
求证:四边形![]() 是平行四边形;
是平行四边形;
![]() 如图
如图![]() 若四边形
若四边形![]() 是矩形,当
是矩形,当![]() 与
与![]() 重合时,已知
重合时,已知![]() ,且菱形
,且菱形![]() 的面积是
的面积是![]() ,求矩形
,求矩形![]() 的长与宽.
的长与宽.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com