
【题目】一个水库的水位在某段时间内持续上涨,表记录了连续5小时内6个时间点的水位高度,其中![]() 表示时间,
表示时间,![]() 表示水位高度.
表示水位高度.
| 0 | 1 | 2 | 3 | 4 | 5 | … |
| 3 | 3.3 | 3.6 | 3.9 | 4.2 | 4.5 | … |
(1)通过观察数据,请写出水位高度![]() (米)与时间
(米)与时间![]() (小时)的函数解析式(不需要写出定义域);
(小时)的函数解析式(不需要写出定义域);
(2)据估计,这种上涨规律还会持续,并且当水位高度达到8米时,水库报警系统会自动发出警报,请预测再过多久系统会发出警报.
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
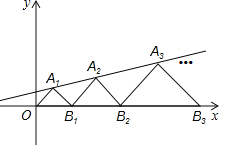
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() ,
,![]() ,…和
,…和![]() ,
,![]() ,
,![]() ,…分别在直线
,…分别在直线![]() 和
和![]() 轴上.
轴上.![]() ,
,![]() ,
,![]() ,…都是等腰直角三角形,它们的面积分别记作
,…都是等腰直角三角形,它们的面积分别记作![]() ,
,![]() ,
,![]() ,…,如果点
,…,如果点![]() 的坐标为
的坐标为![]() ,那么
,那么![]() 的纵坐标为_______.
的纵坐标为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数 | 频数 | 频率 |
0≤x<4000 | 8 | a |
4000≤x<8000 | 15 | 0.3 |
8000≤x<12000 | 12 | b |
12000≤x<16000 | c | 0.2 |
16000≤x<20000 | 3 | 0.06 |
20000≤x<24000 | d | 0.04 |
请根据以上信息,解答下列问题:
(1)写出a,b,c,d的值并补全频数分布直方图;
(2)本市约有37800名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?
(3)若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步的两名教师与大家分享心得,求被选取的两名教师恰好都在20000步(包含20000步)以上的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种进价为每件10元的日用商品,经调查发现,该商品每天的销售量![]() (件)与销售单价
(件)与销售单价![]() (元)满足
(元)满足![]() ,设销售这种商品每天的利润为
,设销售这种商品每天的利润为![]() (元).
(元).
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)在保证销售量尽可能大的前提下,该商场每天还想获得2000元的利润,应将销售单价定为多少元?
(3)当每天销售量不少于50件,且销售单价至少为32元时,该商场每天获得的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,如果一个点的纵坐标恰好是横坐标![]() 倍,那么我们就把这个点定义为“萌点”.
倍,那么我们就把这个点定义为“萌点”.
(1)若点![]() 的坐标分别为
的坐标分别为![]() ,则四边形
,则四边形![]() 四条边上的“萌点”坐标是___.
四条边上的“萌点”坐标是___.
(2)若一次函数![]() 的图像上有一个“萌点”的横坐标是-3,求k值;
的图像上有一个“萌点”的横坐标是-3,求k值;
(3)若二次函数![]() 的图像上没有“萌点”,求k的取值范围.
的图像上没有“萌点”,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为8,M是AB的中点,P是BC边上的动点,连结PM,以点P为圆心,PM长为半径作![]() .当
.当![]() 与正方形ABCD的边相切时,BP的长为( )
与正方形ABCD的边相切时,BP的长为( )
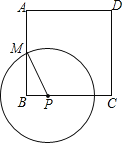
A. 3B. ![]() C. 3或
C. 3或![]() D. 不确定
D. 不确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆每年夏季推出两种游泳付费方式.方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费4元;方式二:不购买会员证,每次游泳付费10元.设小明计划今年夏季游泳次数为x(x为正整数).
(1)根据题意,填写下表:
游泳次数 | 10 | 15 | 20 | … | x |
方式一的总费用(元) | 140 | 160 | _______ | … | _______ |
方式二的总费用(元) | 100 | 150 | ________ | … | ________ |
(2)若小明计划今年夏季游泳的总费用为260元,选择哪种付费方式,他游泳的次数比较多?
(3)小明选择哪种付费方式更合算?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明对![]() ,
,![]() ,
,![]() ,
,![]() 四个中小型超市的女工人数进行了统计,并绘制了下面的统计图表,已知
四个中小型超市的女工人数进行了统计,并绘制了下面的统计图表,已知![]() 超市有女工20人.所有超市女工占比统计表
超市有女工20人.所有超市女工占比统计表
超市 |
|
|
|
|
女工人数占比 | 62.5% | 62.5% | 50% | 75% |
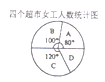
(1)![]() 超市共有员工多少人?
超市共有员工多少人?![]() 超市有女工多少人?
超市有女工多少人?
(2)若从这些女工中随机选出一个,求正好是![]() 超市的概率;
超市的概率;
(3)现在![]() 超市又招进男、女员工各1人,
超市又招进男、女员工各1人,![]() 超市女工占比还是75%吗?甲同学认为是,乙同学认为不是.你认为谁说的对,并说明理由.
超市女工占比还是75%吗?甲同学认为是,乙同学认为不是.你认为谁说的对,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
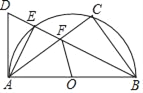
【题目】如图,以AB为直径作半圆O,点C是半圆上一点,∠ABC的平分线交⊙O于E,D为BE延长线上一点,且∠DAE=∠FAE.
(1)求证:AD为⊙O切线;
(2)若sin∠BAC=![]() ,求tan∠AFO的值.
,求tan∠AFO的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com