
【题目】计算:
(1)![]()
;
(2)(x-1)2-(x+1)(x-3).
【答案】
(1)
解:原式=![]() -1-
-1-![]() +2
+2
=1-![]() .
.
(2)
解:原式=x2-2x+1-(x2-2x-3)
=x2-2x+1-x2+2x+3
=4.
【解析】本题考查实数的运算以及多项式乘多项式、完全平方公式,熟练掌握相应定义及运算法则是解题关键.
【考点精析】根据题目的已知条件,利用整数指数幂的运算性质和多项式乘多项式的相关知识可以得到问题的答案,需要掌握aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数);多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加.


科目:初中数学 来源: 题型:
【题目】为了对一棵倾斜的古杉树AB进行保护,需测量其长度.如图,在地面上选取一点C,测得∠ACB=45°,AC=21m,∠BAC=53°,求这颗古杉树AB的长度. (参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)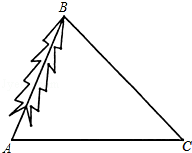
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,面积为24的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上.若BF= ![]() ,则小正方形的周长为( )
,则小正方形的周长为( ) 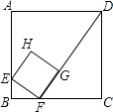
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于代数式x2-10x+24,下列说法:①它是二次三项式; ②该代数式的值可能等于2017;③分解因式的结果是(x-4)(x-6);④该代数式的值可能小于-1.其中正确的有( )
A.1个
B.2个
C.3 个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个正两位数的个位数字是a,十位数字比个位数字大2.
(1)列式表示这个两位数;
(2)把这个两位数的十位上的数字与个位上的数字交换位置得到一个新的两位数,试说明新数与原数的和能被22整除.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ACD和Rt△BEC中,若AD=BE,DC=EC,则不正确的结论是( )

A. Rt△ACD和Rt△BCE全等 B. OA=OB
C. E是AC的中点 D. AE=BD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某容器由A、B、C三个连通长方体组成,其中A、B、C的底面积分别为25cm2、10cm2、5cm2,C的容积是整个容器容积的![]() (容器各面的厚度忽略不计),A、B的总高度为12厘米.现以均匀的速度(单位:cm3/min)向容器内注水,直到注满为止.已知单独注满A、B分别需要的时间为10分钟、8分钟.
(容器各面的厚度忽略不计),A、B的总高度为12厘米.现以均匀的速度(单位:cm3/min)向容器内注水,直到注满为止.已知单独注满A、B分别需要的时间为10分钟、8分钟.
(1)求注满整个容器所需的总时间;
(2)设容器A的高度为xcm,则容器B的高度为 cm;
(3)求容器A的高度和注水的速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上有三个点![]() 、
、![]() 、
、![]() ,如图所示.
,如图所示.
![]()
(1)将点![]() 向左平移4个单位,此时该点表示的数是________;
向左平移4个单位,此时该点表示的数是________;
(2)将点![]() 向左平移3个单位得到数
向左平移3个单位得到数![]() ,再向右平移2个单位得到数
,再向右平移2个单位得到数![]() ,则
,则![]() ,
,![]() 分别是多少?
分别是多少?
(3)怎样移动![]() 、
、![]() 、
、![]() 中的两点,使三个点表示的数相同?你有几种方法?
中的两点,使三个点表示的数相同?你有几种方法?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在直角坐标系xOy中,点A在y轴上,点B,点C在x轴上,点C在点B的右侧,OA=2OB=2BC=2.
(1)点C的坐标是 ;
(2)点P是x轴上一点,点P到AC的距离等于AC的长度,求点P的坐标;
(3)如图2,点D是AC上一点,∠CBD=∠ABO,连接OD,在AB上是否存在一点Q,使QB=AB﹣OD,若存在,求点Q与点D的横坐标之和,若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com