
【题目】为了对一棵倾斜的古杉树AB进行保护,需测量其长度.如图,在地面上选取一点C,测得∠ACB=45°,AC=21m,∠BAC=53°,求这颗古杉树AB的长度. (参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)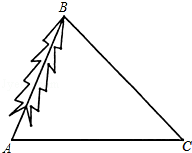
科目:初中数学 来源: 题型:
【题目】材料:
一般地,n个相同的因数a相乘:![]() 记为
记为![]() .如23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).
.如23=8,此时,3叫做以2为底8的对数,记为log28(即log28=3).
一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).如34=81,则4叫做以3为底81的对数,记为log381(即log381=4).
问题:
(1)计算以下各对数的值:log24=______,log216=______,log264=______.
(2)观察(1)中三数4、16、64之间满足怎样的关系式为______log24、log216、log264之间又满足怎样的关系式:______
(3)由(2)的结果,你能归纳出一个一般性的结论吗?logaM+logaN=______(a>o且a≠1,M>0,N>0).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四张完全相同的卡片上,分别画有圆、菱形、等腰三角形正六边形,现从中随机抽取一张,卡片上的图形是中心对称图形的概率是( )
A.![]()
B.![]()
C.![]()
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,点A、B分别在x轴正半轴上,且线段OA、OB(OA<OB)的长分别等于方程![]() 的两个根,点C在
的两个根,点C在![]() 轴正半轴上,且OB=2OC.
轴正半轴上,且OB=2OC.
(1)求A、B、C三点坐标;
(2)将△OBC绕点C顺时针旋转90°后得到![]() ,求直线
,求直线![]() 的表达式.
的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.若AE=1,则FM的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(图1),后人称其为“赵爽弦图”,由弦图变化得到图2,它是用八个全等的直角三角形拼接而成,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为S1、S2、S3.若S1+S2+S3=12,则S2的值为_______.
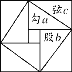
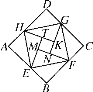
(图1) (图2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级进行法律知识竞赛,共有30道题,答对一道题得4分,不答或答错一道题扣2分.
(1)小红同学参加了竞赛,成绩是96分,请问小红在竞赛中答对了多少题?
(2)小明也参加了竞赛,考完后他说:“这次竟赛中我一定能拿到110分.”请问小明有没有可能拿到110分?试用方程的知识来说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“WJ一号”水稻种子,当年种植,当年收割,当年出水稻产量,(以后每年要出产量还需重要新种植),某村2014、2015、2016年连续尝试种植了此水稻种子.2015年和2016年种植面积都比上年减少相同的数量,若2016年平均每公顷水稻产量比2015年增加的百分数是2015年比2014年增加的百分数的1.25倍,2016年比2014年种植面积减少的百分数与2016年水稻总产量比2014年增加的百分数相同,都等于2015年比上年平均每公顷水稻产量增加的百分数.
(1)求2016年平均每公顷水稻产量比2015年增加的百分数;
(2)求2015年这种水稻总产量比上年增加的百分数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com