
 ��֪ƽ��ֱ������ϵxOy����ͼ����˫����y=$\frac{k}{x}$��k��0����ֱ��y=x+2��������A��2��m����
��֪ƽ��ֱ������ϵxOy����ͼ����˫����y=$\frac{k}{x}$��k��0����ֱ��y=x+2��������A��2��m�������� ��1���ɰ�A���������ֱ�߽���ʽ���m���ٰ�A��������뷴������������ʽ�����k��
��2���������B�����꣬�����ֱ��BC�ķ��̣������C�����꣬���жϡ�ABCΪֱ�������Σ�������������
��3�������D�����꣬�����AD��CD��AC�����������ֻ�С�ACD�ס�CAE���������������ε����ʿ����CE�������E�����꣬��ʾ��CE���������E�����꣮
��� �⣺��1����ֱ��y=x+2��������A��2��m����
��m=2+2=4����A��2��4����
��˫����y=$\frac{k}{x}$��k��0��������A��
��k=2��4=8��
��2����˫���߾�����B��n��2����
��2n=8�����n=4��
��B��4��2����
���������ֱ��BC����ʽΪy=x+b��
��B���������ɵ�2=4+b�����b=-2��
��ֱ��BC����ʽΪy=x-2��
��C��0��-2����
��AC=$\sqrt{��2-0��^{2}+[4-��-2��]^{2}}$=$\sqrt{40}$=2$\sqrt{10}$��BC=$\sqrt{��4-0��^{2}+[2-��-2��]^{2}}$=$\sqrt{32}$=4$\sqrt{2}$��AB=$\sqrt{��4-2��^{2}+��2-4��^{2}}$=$\sqrt{8}$=2$\sqrt{2}$��
��BC2+AB2=AC2��
���ABC����ACΪб�ߵ�ֱ�������Σ�
��S��ABC=$\frac{1}{2}$AB•BC=$\frac{1}{2}$��2$\sqrt{2}$��4$\sqrt{2}$=8��
��3����ֱ��y=x+2��y�ύ�ڵ�D��
��D��0��2����
��AD=$\sqrt{��2-0��^{2}+��4-2��^{2}}$=2$\sqrt{2}$����AC=2$\sqrt{10}$
��ͼ��ʾ��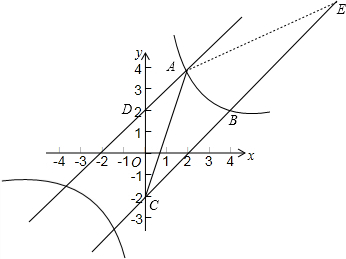
��AD��CE��
���DAC=��ACE��
����ACD=��EAC����AE��CD���ı���AECDΪƽ���ı��Σ���ʱ��ADC�ա�CEA��������������
���ACD=��AEC��
���ACD�ס�CAE��
��$\frac{AD}{AC}$=$\frac{AC}{CE}$����$\frac{2\sqrt{2}}{2\sqrt{10}}$=$\frac{2\sqrt{10}}{CE}$�����CE=10$\sqrt{2}$��
��E����ֱ��BC�ϣ�
�����E��x��x-2����x��0����
�֡�C��0��-2����
��CE=$\sqrt{��x-0��^{2}+[x-2-��-2��]^{2}}$=$\sqrt{2}$x��
��$\sqrt{2}$x=10$\sqrt{2}$�����x=10��
��E��������10��8����
���� ������Ҫ���鷴�����������ۺ�Ӧ�ã��漰֪ʶ���д���ϵ������������ʽ��ֱ�������ε��ж���ƽ���ı��ε����ʡ����������ε��ж������ʵȣ��ڣ�1����ע�ⷴ����������k=xy��Ӧ�ã��ڣ�2�����ж���ABCΪֱ���������ǽ���Ĺؼ����ڣ�3���и����������CE�ij��ǽ���Ĺؼ��������漰֪ʶ��϶࣬�ۺ��Խ�ǿ���ѶȽϴ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | 7 | C�� | 9 | D�� | 12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���εĶԽ�����ƽ������� | |
| B�� | ���εĶԽ����ഹֱƽ�� | |
| C�� | �Խ�������Ҵ�ֱ���ı����������� | |
| D�� | �Խ�����ƽ�ֵ��ı�����ƽ���ı��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
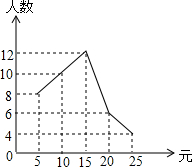 ij��40��ѧ���μ���һ�Ρ��װ���һ�վ衱�����������������ͼ��ʾ������ͼ�����ṩ����Ϣ������Ϊ��ξ����40���������λ����15Ԫ��
ij��40��ѧ���μ���һ�Ρ��װ���һ�վ衱�����������������ͼ��ʾ������ͼ�����ṩ����Ϣ������Ϊ��ξ����40���������λ����15Ԫ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 12Ԫ��12Ԫ | B�� | 12Ԫ��11Ԫ | C�� | 11.6Ԫ��12Ԫ | D�� | 11.6Ԫ��11Ԫ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
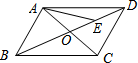 ��ͼ����?ABCD�У�AC��BD�ཻ�ڵ�O����E��OD ���е㣬��$\overrightarrow{BA}$=$\overrightarrow{a}��\;\overrightarrow{BC}$=$\overrightarrow{b}$����ô$\overrightarrow{AE}$=$\frac{3}{4}$$\overrightarrow{b}$-$\frac{1}{4}$$\overrightarrow{a}$��
��ͼ����?ABCD�У�AC��BD�ཻ�ڵ�O����E��OD ���е㣬��$\overrightarrow{BA}$=$\overrightarrow{a}��\;\overrightarrow{BC}$=$\overrightarrow{b}$����ô$\overrightarrow{AE}$=$\frac{3}{4}$$\overrightarrow{b}$-$\frac{1}{4}$$\overrightarrow{a}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵxOy�У�������y=ax2+bx+c����A��-1��0����B��3��0����C��2��3�����㣬����y�ύ�ڵ�D��
��ͼ����ƽ��ֱ������ϵxOy�У�������y=ax2+bx+c����A��-1��0����B��3��0����C��2��3�����㣬����y�ύ�ڵ�D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
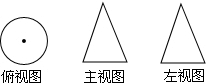 ��ͼ��ʾij�����������ͼ��������������ǣ�������
��ͼ��ʾij�����������ͼ��������������ǣ�������| A�� | ���� | B�� | Բ�� | C�� | �� | D�� | Բ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com