
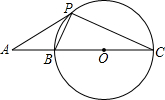
 如图,点A、B、C在同一条直线上,点P在以BC为直径的⊙O上,连结PA、PB、PC,AB=BP=$\frac{1}{2}BC$.
如图,点A、B、C在同一条直线上,点P在以BC为直径的⊙O上,连结PA、PB、PC,AB=BP=$\frac{1}{2}BC$.分析 (1)连接OP,进而得出AB=BP=BO,进而得出∠BPA+∠BPO=90°,即可得出答案;
(2)利用已知首先求出BP的长,再利用勾股定理得出PC的长即可.
解答  解:(1)如图所示:连接OP,
解:(1)如图所示:连接OP,
∵AB=BP=$\frac{1}{2}$BC,BC为直径,
∴AB=BP=BO,
∴∠BAP=∠BPA,∠BPO=∠BOP,
∴∠BAP+∠BPA+∠BPO+∠BOP=180°,
∴∠BPA+∠BPO=90°,
∵点P在⊙O上,
∴AP是⊙O的切线;
(2)∵BC为直径,
∴BC=4cm,∠BPC=90°,
∵BP=$\frac{1}{2}$BC,
∴BP=2,
在Rt△BPC中,由勾股定理得:
PC=$\sqrt{P{C}^{2}-B{P}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴PC的长度为2$\sqrt{3}$cm.
点评 此题主要考查了切线的判定以及勾股定理、等腰三角形的性质等知识,正确得出∠BPA+∠BPO=90°是解题关键.


 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}+\sqrt{3}$=$\sqrt{5}$ | B. | 4x2y-x2y=4 | C. | a3•a4=a12 | D. | (a2b)3=a6b3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 年龄(岁) | 13 | 14 | 15 | 16 |
| 人数 | 3 | 16 | 19 | 2 |
| A. | 19,15 | B. | 15,14.5 | C. | 19,14.5 | D. | 15,15 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
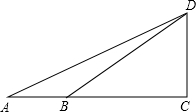 小明准备用所学数学知识测量广场上旗杆CD的高度,如图所示,在底面A处测得顶端的仰角为25.5°,在B处测得仰角为36.9°,已知点A、B、C在同一直线上,量得AB=10米.求旗杆的高度.(结果保留一位小数,参考数据:sin25.5°≈0.43,cos25.5°≈0.90,tan25.5°≈0.48;sin36.9°≈0.60,cos36.9°≈0.80,tan36.9°≈0.75.)
小明准备用所学数学知识测量广场上旗杆CD的高度,如图所示,在底面A处测得顶端的仰角为25.5°,在B处测得仰角为36.9°,已知点A、B、C在同一直线上,量得AB=10米.求旗杆的高度.(结果保留一位小数,参考数据:sin25.5°≈0.43,cos25.5°≈0.90,tan25.5°≈0.48;sin36.9°≈0.60,cos36.9°≈0.80,tan36.9°≈0.75.)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com