
分析 分两种情况分别作图,再根据题设和结论写出已知和求证,根据平行线的性质,可证明结论.
解答 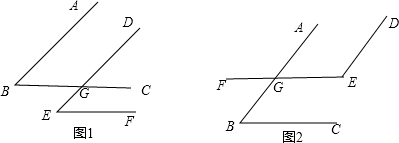 已知:如图,AB∥DE,BC∥EF;
已知:如图,AB∥DE,BC∥EF;
求证:∠ABC=∠DEF或∠ABC+∠DEF=180°,
证明:
在图1中,∵AB∥DE,
∴∠ABC=∠DGC,
∵BC∥EF,
∴∠DGC=∠DEF,
∴∠ABC=∠DEF;
在图2中,∵AB∥DE,
∴∠DEF+∠AGE=180°,
∵BC∥EF,
∴∠AGE=∠ABC,
∴∠ABC+∠DEF=180°,
即如果一个角的两条边与另一个角的两条边分别平行,则这两个角相等或互补.
故答案为:
如图,AB∥DE,BC∥EF;
∠ABC=∠DEF或∠ABC+∠DEF=180°;
在图1中,∵AB∥DE,
∴∠ABC=∠DGC,
∵BC∥EF,
∴∠DGC=∠DEF,
∴∠ABC=∠DEF;
在图2中,∵AB∥DE,
∴∠DEF+∠AGE=180°,
∵BC∥EF,
∴∠AGE=∠ABC,
∴∠ABC+∠DEF=180°,
即如果一个角的两条边与另一个角的两条边分别平行,则这两个角相等或互补.
点评 本题主要考查平行线的性质,掌握平行线的性质和判定是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c⇒a∥c.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
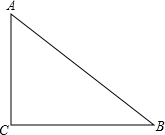 已知,直角△ABC中,∠C=90°,AC=6cm,BC=8cm,将△ABC沿C到B方向平移2cm后得到△A′B′C′,A′C′交AB于点D.
已知,直角△ABC中,∠C=90°,AC=6cm,BC=8cm,将△ABC沿C到B方向平移2cm后得到△A′B′C′,A′C′交AB于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
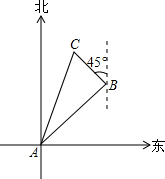 如图,在一次实践活动中,聪聪从A地出发,沿北偏东45°方向行进了4$\sqrt{3}$千米到达B地,然后再沿北偏西45°方向行进了4km到达目的地点C.
如图,在一次实践活动中,聪聪从A地出发,沿北偏东45°方向行进了4$\sqrt{3}$千米到达B地,然后再沿北偏西45°方向行进了4km到达目的地点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com