
分析 (1)已知一次函数y=x+m与反比例函数y2=$\frac{m+1}{x}$(m≠-1)的图象在第一象限内的交点为P(x0,3),把P点的坐标代入两个解析式就可以解决;
(2)先求得交点坐标,然后根据函数的图象找出一次函数的图象在反比例函数的图象上方部分即可.
解答 解:(1)∵点P(x0,3)在一次函数y=x+m的图象上.
∴3=x0+m,即m=3-x0.
又∵点P(x0,3)在反比例函数y2=$\frac{m+1}{x}$(m≠-1)的图象上,
∴3=$\frac{m+1}{{x}_{0}}$,即m=3x0-1.
∴3-x0=3x0-1,
解得x0=1;
∴P(1,3),
代入y1=x+m得,3=1+m,
∴m=2,
∴一次函数的解析式为y=x+2,反比例函数的解析式为y=$\frac{3}{x}$;
(2)解$\left\{\begin{array}{l}{y=x+2}\\{y=\frac{3}{x}}\end{array}\right.$得$\left\{\begin{array}{l}{x=-3}\\{y=-1}\end{array}\right.$或$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$
∴一次函数和反比例函数的交点坐标(1,3)和(-3,-1),
如图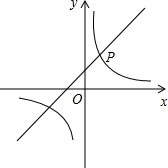
由图象知,满足题意的x的取值范围为:-3<x<0或x>1.
点评 本题考查了函数的图象与解析式的关系:点在图象上,就一定满足函数的解析式.同时还考查了利用待定系数法求函数解析式的方法.


科目:初中数学 来源: 题型:选择题
| A. | 232-1 | B. | 232+1 | C. | $\frac{{{2^{32}}-1}}{3}$ | D. | $\frac{{{2^{32}}-1}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
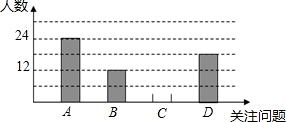 6月5日是世界环境日,中国每年都有鲜明的主题,旨在释放和传递:建设美丽中国,人人共享,人人有责的信息,小明积极学习与宣传,并从四个方面A-空气污染,B-淡水资源危机,C-土地荒漠化,D-全球变暖,对全校同学进行了随机抽样调查,了解他们在这四个方面中最关注的问题(每人限选一项),以下是他收集数据后,绘制的不完整的统计图表:
6月5日是世界环境日,中国每年都有鲜明的主题,旨在释放和传递:建设美丽中国,人人共享,人人有责的信息,小明积极学习与宣传,并从四个方面A-空气污染,B-淡水资源危机,C-土地荒漠化,D-全球变暖,对全校同学进行了随机抽样调查,了解他们在这四个方面中最关注的问题(每人限选一项),以下是他收集数据后,绘制的不完整的统计图表:| 关注问题 | 频数 | 频率 |
| A | 24 | b |
| B | 12 | 0.2 |
| C | n | 0.1 |
| D | 18 | m |
| 合计 | a | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
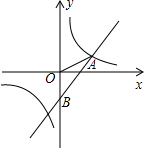 如图,已知在平面直角坐标系中,O是坐标原点,点A(3,1)是反比例函数y1=$\frac{k}{x}$与一次函数y2=x+b的交点,点B是一次函数与y轴的交点.
如图,已知在平面直角坐标系中,O是坐标原点,点A(3,1)是反比例函数y1=$\frac{k}{x}$与一次函数y2=x+b的交点,点B是一次函数与y轴的交点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
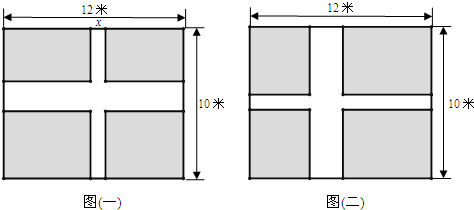
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
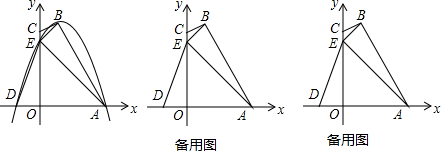
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com