
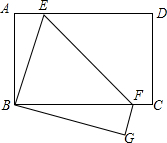
 已知,如图,矩形ABCD边AB=6,BC=8,再沿EF折叠,使D点与B点重合,C点的对应点为G,将△BEF绕着点B顺时针旋转,旋转角为a(0°<a<180°),记旋转这程中的三角形为△BE′F′,在旋转过程中设直线E′F′与射钱EF,射线ED分别交于点M、N,当EN=MN时,则FM的长为$\frac{5}{4}$.
已知,如图,矩形ABCD边AB=6,BC=8,再沿EF折叠,使D点与B点重合,C点的对应点为G,将△BEF绕着点B顺时针旋转,旋转角为a(0°<a<180°),记旋转这程中的三角形为△BE′F′,在旋转过程中设直线E′F′与射钱EF,射线ED分别交于点M、N,当EN=MN时,则FM的长为$\frac{5}{4}$. 分析 设AE=x=FC=FG,则BE=ED=8-x,由勾股定理得:AB2+AE2=BE2,即62+x2=(8-x)2,解得:x=$\frac{7}{4}$,BE=$\frac{25}{4}$,EF=$\frac{15}{2}$,由折叠性质得:∠BEF=∠DEF=∠BFE,得出∠DEF=∠NME=∠F′,证得四边形BEMF′为平行四边形,由BE=BF′,证得平行四边形BEMF′为菱形,得出EM=BE=$\frac{25}{4}$,即可得出结果.
解答 解:如图所示: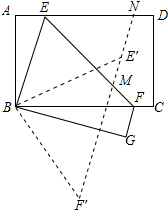
由折叠性质得:设AE=x=FC=FG,
则BE=ED=8-x,
在Rt△ABE中,由勾股定理得:AB2+AE2=BE2,
即62+x2=(8-x)2,
解得:x=$\frac{7}{4}$,
∴BE=8-$\frac{7}{4}$=$\frac{25}{4}$,
EF=$\sqrt{(BC-AE-FC)^{2}+A{B}^{2}}$=$\sqrt{(8-2x)^{2}+{6}^{2}}$=$\frac{15}{2}$,
由折叠性质得:∠BEF=∠DEF=∠BFE,
∵EN=NM,
∴∠DEF=∠NME=∠F′,
∴EM∥BF′,BE∥E′F′,
∴四边形BEMF′为平行四边形,
由旋转性质得:BF′=BF=8-x,
∴BE=BF′,
∴平行四边形BEMF′为菱形,
∴EM=BE=$\frac{25}{4}$,
∴FM=EF-EM=$\frac{15}{2}$-$\frac{25}{4}$=$\frac{5}{4}$.
故答案为:$\frac{5}{4}$.
点评 本题考查了旋转的性质、勾股定理、矩形的性质、菱形的判定、平行四边形的判定等知识;本题综合性强,有一定难度,证出四边形BEMF′是菱形是解决问题的关键.


科目:初中数学 来源: 题型:解答题
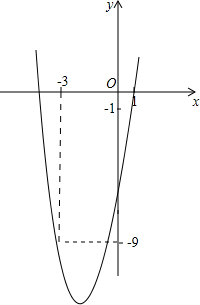 如图,已知二次函数y=ax2+4x+c的图象经过点A(1,-1)和点B(-3,-9).
如图,已知二次函数y=ax2+4x+c的图象经过点A(1,-1)和点B(-3,-9).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
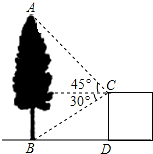 如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为6m,求大树的高度为多少m?(结果保留根号)
如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为6m,求大树的高度为多少m?(结果保留根号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com