练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，点在一条直线上，,∥，．

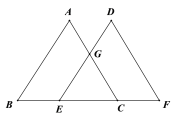
    （1）求证：

    （2）若°，求的大小．

    【答案】（1）详见解析；（2）65°

    【解析】

    （1）由线段的和差得BC=EF，平行线的性质得∠B=∠DEC，角边角证明△ABC≌△DEF，由全等性质得AC=DF；

    （2）由全等三角形的性质得∠F=∠ACB，同位角相等证明∠D=∠EGC，根据平行线的性质和等量代换求得∠EGC=65°．

    （1）证明：∵BC=BE+EC，EF=CF+EC，BE=CF，

    ∴BC=EF，

    又∵AB∥DE，

    ∴∠B=∠DEC，

    在△ABC和△DEF中，

    ，

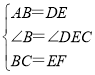    ∴△ABC≌△DEF（SAS），

    ∴AC=DF；

    （2）解：∵△ABC≌△DEF，

    ∴∠F=∠ACB，

    ∴DF∥AC，

    ∴∠D=∠EGC，

    又∵∠D=65°，

    ∴∠EGC=65°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】学校今年组织学生参加志愿者活动，活动分为甲、乙、丙三组进行．下面的条形统计图和扇形统计图反映了学生参加活动的报名情况，请你根据图中的信息，解答下列问题：

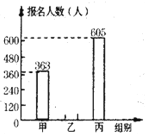
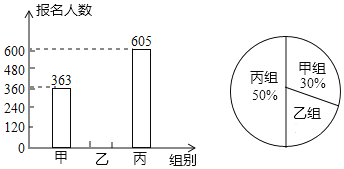
    （1）若在参加活动的学生中随机抽取一名学生，则抽到乙组学生的概率是

    （2）今年参加志愿者共 人，并把条形统计图补充完整；

    （3）学校两年前参加志愿者的总人数是810人，若这两年的年增长率相同，求这个年增长率．（精确到1%）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

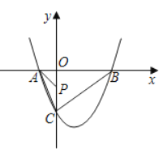
    【题目】如图，已知二次函数的图象交轴于，两点，交轴于点，其中.

    （1）求点的坐标，并用含的式子表示；

    （2）连接，，当为锐角时，求的取值范围；

    （3）若为轴上一个动点，连接，当点的坐标为时，直接写出的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

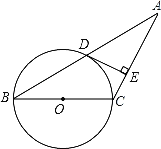
    【题目】如图，在等腰△ABC中，AC＝BC，以BC为直径的⊙O与底边AB交于点D，过D作⊙O的切线交AC于点E．

    （1）证明：DE⊥AC．

    （2）若BC＝8，AD＝6，求AE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】学校数学社团的同学们在学生中开展“了解校训意义”的调查活动．采取随机抽样的方式进行问卷调查．问卷调查的结果分为、、、四类．类表示非常了解；类表示比较了解；类表示基本了解；类表示不太了解．（要求每位同学必须选并且只能选择一项）统计数据整理如表：

    类别

    频数

    频率

    20

    0.3

    11

    0.22

    4

    0.08

    （1）表中__________；_________．

    （2）根据表中数据，求出类同学数所对应的扇形圆心角为_________度．

    （3）根据调查结果，请你估计该校1500名学生中对校训“非常了解”的人数；

    （4）学校在开展了解校训意义活动中，需要从类的甲、乙、丙、丁四名同学中随机选取2人参加展示活动，求恰好选中甲乙两人的概率？（请用列表法或是树状图表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平行四边形ABCD中，以点A为圆心，AB长为半径画弧交AD于点F，再分别以点B、F为圆心，大于BF的长为半径画弧，两弧交于点P；连接AP并延长交BC于点E，连接EF．若四边形ABEF的周长为12，∠C＝60°，则四边形ABEF的面积是（　　）

    A.9B.12C.D.6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若一个函数当自变量在不同范围内取值时，函数表达式不同，我们称这样的函数为分段函数，下面我们参照学习函数的过程与方法，探究分段函数y＝的图象与性质，探究过程如下，请补充完整．

    （1）列表：

    x

    …

    -4

    -3

    -2

    -1

    0

    1

    2

    3

    4

    …

    y

    …

    3

    m

    1

    0

    1

    2

    1

    n

    …

    其中，m＝　 ，n＝　 　．

    （2）描点：在平面直角坐标系中，以自变量x的取值为横坐标，以相应的函数值y为纵坐标，描出相应的点，如图所示，请画出函数的图象．

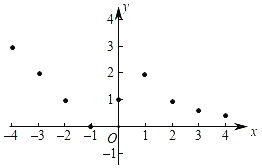
    （3）研究函数并结合图象与表格，回答下列问题：

    ①点A（，y1），B（5，y2），C（x1，），D（x2，6）在函数图象上，则y1　 y2，x1　 x2；（填“＞”，“＝”或“＜”）

    ②当函数值y＝1时，求自变量x的值；

    （4）若直线y＝﹣x+b与函数图象有且只有一个交点，请直接写出b的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB＝AC，D为BC中点，点E是BA延长线上一点，点F是AC上一点，连接EF并延长交BC于点G，且AE＝AF．

    （1）若∠ABC＝50°．求∠AEF的度数；

    （2）求证：AD∥EG．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一般地，对于已知一次函数y1=ax+b，y2=cx+d（其中a，b，c，d为常数，且ac＜0），定义一个新函数y=，称y是y1与y2的算术中项，y是x的算术中项函数．

    （1）如：一次函数y1=x﹣4，y2=﹣x+6，y是x的算术中项函数，即y=．

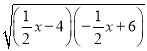    ①自变量x的取值范围是　 　，当x=　 　时，y有最大值；

    ②根据函数研究的途径与方法，请填写下表，并在图1中描点、连线，画出此函数的大致图象；

    x

    8

    9

    10

    12

    13

    14

    16

    17

    18

    y

    0

    1.2

    1.6

    　 　

    2.04

    2

    　 　

    1.2

    0

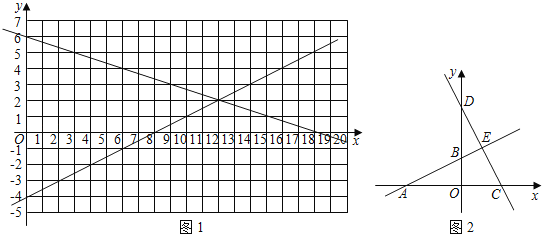
    ③请写出一条此函数可能有的性质　 　；

    （2）如图2，已知一次函数y1=x+2，y2=﹣2x+6的图象交于点E，两个函数分别与x轴交于点A，C，与y轴交于点B，D，y是x的算术中项函数，即y=．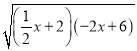

    ①判断：点A、C、E是否在此算术中项函数的图象上；

    ②在平面直角坐标系中是否存在一点，到此算术中项函数图象上所有点的距离相等，如果存在，请求出这个点；如果不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案