
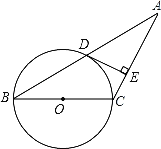
【题目】如图,在等腰△ABC中,AC=BC,以BC为直径的⊙O与底边AB交于点D,过D作⊙O的切线交AC于点E.
(1)证明:DE⊥AC.
(2)若BC=8,AD=6,求AE的长.
【答案】(1)详见解析;(2)AE=![]() .
.
【解析】
(1)连接OD,根据DE是⊙O的切线,可得∠ODE=90°,由AC=BC,可得∠OBD=∠A,进而可得∠A=∠ODB,可得OD∥AC,即可证明结论;
(2)连接CD,根据BC为直径,证明△ADE∽△ACD,对应边成比例即可求出AE的长.
解:(1)如图,连接OD,
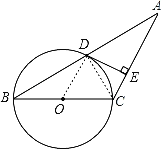
∵DE是⊙O的切线,
∴∠ODE=90°,
∵OB=OD,
∴∠OBD=∠ODB,
∵AC=BC,
∴∠OBD=∠A,
∴∠A=∠ODB,
∴OD∥AC,
∴∠DEC=90°,
即DE⊥AC.
(2)连接CD,
∵BC为直径,
∴∠BDC=∠CDA=90°,
∴∠DEA=∠CDA=90°,
∵∠A=∠A,
∴△ADE∽△ACD,
∴![]() ,即
,即![]() ,
,
∴AE=![]() .
.


科目:初中数学 来源: 题型:
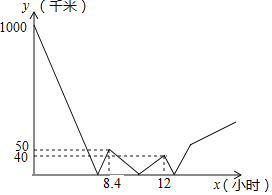
【题目】在同一直线上有A、B两地,甲车从A地送货到B地,同时乙车从B地前往A地,两车皆匀速行驶.途中某一时刻,甲车发现有货物落在A、B之间的某处C地,于是立刻掉头并以自己原来速度的两倍匀速返回,取到货物后,再以最初的速度继续匀速向B地行驶.两车之间的距离y(千米)与甲车行驶的时间x(小时)之间的函数关系如图所示(途中掉头、取货物耽误时间忽略不计),当乙车到达A地时,甲车到A地的距离为_____千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家规定,中小学生每天在校体育活动时间不低于1小时.为了解这项政策的落实情况,有关部门就“你某天在校体育活动时间是多少”的问题,在某校随机抽查了部分学生,再根据活动时间![]() (小时)进行分组(A组:
(小时)进行分组(A组:![]() ,B组:
,B组:![]() ,C组:
,C组:![]() ,D组:
,D组:![]() ),绘制成如下两幅统计图,请根据图中信息回答问题:
),绘制成如下两幅统计图,请根据图中信息回答问题:
(1)此次抽查的学生数为________人;
(2)补全条形统计图;

(3)从抽查的学生中随机询问一名学生,该生当天在校体育活动时间低于1小时的概率是__________;
(4)若当天在校学生数为1200人,请估计在当天达到国家规定体育活动时间的学生有__________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ACB中,∠ACB=90°,AC=2BC=4,点P为AB边中点,点E为AC边上不与端点重合的一动点,将△ADP沿着直线PD折叠得△PDE,若DE⊥AB,则AD的长度为_____ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,直线![]() 交坐标轴于A、C两点,抛物线
交坐标轴于A、C两点,抛物线![]() 过A、C两点.
过A、C两点.
(1)求抛物线的解析式;
(2)若点P为抛物线位于第三象限上一动点,连接PA,PC,试问△PAC是否存在最大值,若存在,请求出△APC取最大值以及点P的坐标,若不存在,请说明理由;
(3)点M为抛物线上一点,点N为抛物线对称轴上一点,若△NMC是以∠NMC为直角的等腰直角三角形,请直接写出点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
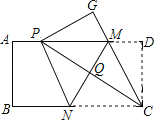
【题目】如图,先有一张矩形纸片![]() 点
点![]() 分别在矩形的边
分别在矩形的边![]() 上,将矩形纸片沿直线MN折叠,使点
上,将矩形纸片沿直线MN折叠,使点![]() 落在矩形的边
落在矩形的边![]() 上,记为点
上,记为点![]() ,点
,点![]() 落在
落在![]() 处,连接
处,连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .下列结论:
.下列结论:
![]()
②四边形![]() 是菱形;
是菱形;
③![]() 重合时,
重合时,![]() ;
;
④![]() 的面积
的面积![]() 的取值范围是
的取值范围是![]()
其中正确的是_____(把正确结论的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
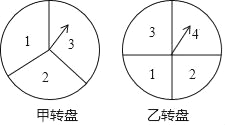
【题目】如图,甲分为三等分数字转盘,乙为四等分数字转盘,自由转动转盘.
(1)转动甲转盘,指针指向的数字小于3的概率是 ;
(2)同时自由转动两个转盘,用列举的方法求两个转盘指针指向的数字均为奇数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一段6000米的道路由甲乙两个工程队负责完成.已知甲工程队每天完成的工作量是乙工程队每天完成工作量的2倍,且甲工程队单独完成此项工程比乙工程队单独完成此项工程少用10天.
(1)求甲、乙两工程队每天各完成多少米?
(2)如果甲工程队每天需工程费7000元,乙工程队每天需工程费5000元,若甲队先单独工作若干天,再由甲乙两工程队合作完成剩余的任务,支付工程队总费用不超过79000元,则两工程队最多可以合作施工多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com