
����Ŀ����һ���������Ա����ڲ�ͬ��Χ��ȡֵʱ����������ʽ��ͬ�����dz������ĺ���Ϊ�ֶκ������������Dz���ѧϰ�����Ĺ����뷽����̽���ֶκ���y�� ��ͼ�������ʣ�̽���������£��벹��������
��ͼ�������ʣ�̽���������£��벹��������
��1�����
x | �� | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | �� |
y | �� | 3 | m | 1 | 0 | 1 | 2 | 1 | n |
| �� |
����m���� ��n���� ����
��2����㣺��ƽ��ֱ������ϵ�У����Ա���x��ȡֵΪ�����꣬����Ӧ�ĺ���ֵyΪ�����꣬�����Ӧ�ĵ㣬��ͼ��ʾ���뻭��������ͼ��
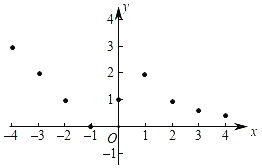
��3���о����������ͼ������ش��������⣺
�ٵ�A��![]() ��y1����B��5��y2����C��x1��
��y1����B��5��y2����C��x1��![]() ����D��x2��6���ں���ͼ���ϣ���y1�� y2��x1�� x2������������������������������
����D��x2��6���ں���ͼ���ϣ���y1�� y2��x1�� x2������������������������������
�ڵ�����ֵy��1ʱ�����Ա���x��ֵ��
��4����ֱ��y����x+b�뺯��ͼ������ֻ��һ�����㣬��ֱ��д��b��ȡֵ��Χ��
���𰸡���1��2��![]() ����2����ͼ��ʾ������������3���٣���������x��0��x����2��x��2����4����1��b��2
����2����ͼ��ʾ������������3���٣���������x��0��x����2��x��2����4����1��b��2![]() ��b��3��
��b��3��
��������
��1����x=��3����y��|x+1|��m��ֵ����x��3����y��![]() �е�n��ֵ��
�е�n��ֵ��
��2����ƽ����������������ϵ����ĵ�ɵã�
��3��A��B��y��![]() �ϣ�C��D��y��|x��1|�ϣ��ֱ���ݺ����������жϣ�
�ϣ�C��D��y��|x��1|�ϣ��ֱ���ݺ����������жϣ�
��4������ͼ������ֱ��y����x+b�뺯��ͼ����һ��������ٽ�㣬�Ӷ��ó�b��ȡֵ��Χ��
��1��x����3����y��|x+1|�ã�y��2��
��m��2��
��x��3����y��![]() �еã�y��
�еã�y��![]() ��
��
��n��![]() ��
��
�ʴ�Ϊ2��![]() ��
��
��2����ͼ��ʾ��
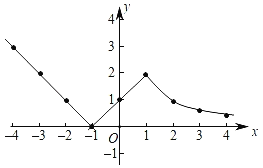
��3����ͼ���֪A��B��y��![]() �ϣ�y��x���������С������y1��y2��
�ϣ�y��x���������С������y1��y2��
C��D��y��|x��1|�ϣ�����x1��x2��
�ʴ�Ϊ��������
����y��1ʱ��x��1ʱ����1��|x+1|��
��x��0��x����2��
��y��1ʱ��x��1ʱ����1��![]() ��
��
��x��2��
��x��0��x����2��x��2��
��4���ߺ�������ʽΪ��y��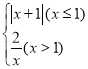 ��ͼ������
��ͼ������

��ֱ��y����x+b������ƽ�ƵĹ����У�����ͼ���뺯���Ľ���������ڱ仯�ģ�
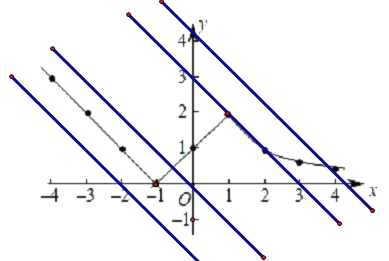
��ͼ�ο�֪����ֱ������ƽ�ƹ����У�ֱ���뺯���������Ϊ����0������Ȼ���Ϊ1������Ȼ���Ϊ2������Ȼ���ֱ�Ϊ1��
���Ƿֱ�����٢ڡ��ڢۡ��ۢ�֮����ٽ�㼴��
��ͼ�ο�֪���٢�֮����ٽ��Ϊ��x=��1
�������ֱ���뺯����2������������
��������ʽ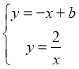 �ã�
�ã�
![]()
������0ʱ����ֱ���뺯��������������
����![]()
���b��2![]() ��b����2
��b����2![]()
�ʶ���1��b��2![]() ʱ��ֱ���뺬�����ҽ���һ������
ʱ��ֱ���뺬�����ҽ���һ������
������һ�����������ͼ
�����������֪��b��2![]() ʱ��ֱ�����뺯����2�������
ʱ��ֱ�����뺯����2�������
���Ƿ�����������ȡֵ��ΧΪx��1�IJ���
������ͼ�������������ǵ�A(1��2)�Ҳ�IJ���
�൱ֱ��y=��x+b��A���������ƽ��ʱ��ֱ���뷴������������һ������
����A����ֱ�ߵã�2=��1+b����ã�b=3
�൱b��3ʱ��ֱ���뺯��Ҳ����һ������
���ϵã���1��b��2![]() ��b��3��
��b��3��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���![]() ��ͼ������κ���
��ͼ������κ���![]() ��ͼ����
��ͼ����![]() ��
��![]() ���㣬��
���㣬��![]() ��
��![]() ���ϣ���
���ϣ���![]() �ĺ�����Ϊ4��
�ĺ�����Ϊ4��
��1��![]() ________��
________��![]() ________��
________��
��2������κ�����ͼ����![]() �ύ��
�ύ��![]() �㣬��
�㣬��![]() �����һ������Ϊ
�����һ������Ϊ![]() ������
������![]() ��
��![]() ����
����![]() ������ֵ��
������ֵ��
��3������![]() ����
����![]() ���·����κ���ͼ���ϣ���
���·����κ���ͼ���ϣ���![]() ����
����![]() ��ƽ���߽�ֱ��
��ƽ���߽�ֱ��![]() �ڵ�
�ڵ�![]() ����
����![]() ��ΪԲ�ģ�
��ΪԲ�ģ�![]() �ij�Ϊ�뾶��Բ����
�ij�Ϊ�뾶��Բ����![]() ��ֱ��
��ֱ��![]() �Ͻصõ��ҳ������ֵ��
�Ͻصõ��ҳ������ֵ��
������ABM=��ACO�����M������Ϊ_________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
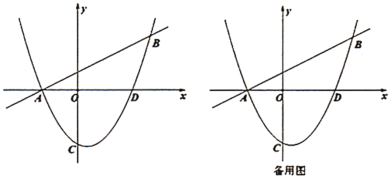
����Ŀ����֪����ͼ��ֱ��![]() ����������A��C���㣬������
����������A��C���㣬������![]() ��A��C���㣮
��A��C���㣮
��1���������ߵĽ���ʽ��
��2������PΪ������λ�ڵ���������һ���㣬����PA��PC�����ʡ�PAC�Ƿ�������ֵ�������ڣ��������APCȡ���ֵ�Լ���P�����꣬�������ڣ���˵�����ɣ�
��3����MΪ��������һ�㣬��NΪ�����߶Գ�����һ�㣬����NMC���ԡ�NMCΪֱ�ǵĵ���ֱ�������Σ���ֱ��д����M�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
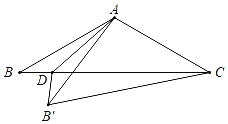
����Ŀ����ͼ������ABC�У�AB��AC��![]() ����B��30����D��BC��һ�㣬����AD������ABD��ֱ��AD�۵�����B����B����������B'C������AB'C��ֱ�������Σ���BD�ij�Ϊ_____��
����B��30����D��BC��һ�㣬����AD������ABD��ֱ��AD�۵�����B����B����������B'C������AB'C��ֱ�������Σ���BD�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
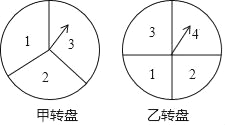
����Ŀ����ͼ����Ϊ���ȷ�����ת�̣���Ϊ�ĵȷ�����ת�̣�����ת��ת�̣�
��1��ת����ת�̣�ָ��ָ�������С��3�ĸ������� ����
��2��ͬʱ����ת������ת�̣����оٵķ���������ת��ָ��ָ������־�Ϊ�����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ס����������С����С����С����һ����ѧ�κ�����һ����ѧʵ�������ͼ����ͬһˮƽ���������������С�������ڵľ���¥��С�������ڵ�С������С���ҵ�һ��Сɽ��ʵ������Ϊ����Сɽ�ĸ߶ȣ���ס��¥��С���ڴ���A�����Сɽɽ����һ�ô�������E�ĸ���Ϊ10����С�����Լ�¥��C�����С���Ҵ���A��������Ϊ37�����Ҳ������CD���¶�i��1��2����֪����ˮƽ����BC��120�ף������߶�DE��3�ף���Сɽɽ��D��ˮƽ��BF�Ĵ�ֱ�߶�ԼΪ�� ������ȷ��0.1�ף��ο�����sin37���![]() ��tan37���
��tan37���![]() ��sin10���
��sin10���![]() ��tan10���
��tan10���![]() ��
��

A.55.0��B.50.3��C.48.1 ��D.57.3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
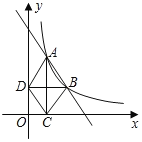
����Ŀ����ͼ����ֱ������ƽ���ڣ�����y=![]() (x��0��m�dz���)��ͼ��A(1��4)��B(a��b)������a��1������A��x�ᴹ�ߣ�����ΪC������B��y�ᴹ�ߣ�����ΪD������AD��DC��CB��
(x��0��m�dz���)��ͼ��A(1��4)��B(a��b)������a��1������A��x�ᴹ�ߣ�����ΪC������B��y�ᴹ�ߣ�����ΪD������AD��DC��CB��
��1�����������Ľ���ʽ��
��2������ABD�����Ϊ4�����B�����ꣻ
��3����֤��DC![]() AB��
AB��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
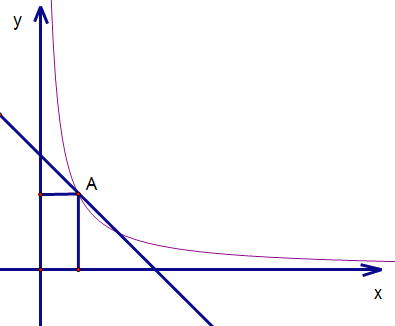
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�ֱ��y��x+4��������y����![]() x2+bx+c��b��c�dz���������A��B���㣬��A��x���ϣ���B��y���ϣ�����������x�����һ������Ϊ��C��
x2+bx+c��b��c�dz���������A��B���㣬��A��x���ϣ���B��y���ϣ�����������x�����һ������Ϊ��C��

��1����������ߵĽ���ʽ��
��2��P����������һ���㣨�����A��B�غϣ���
����ͼ2������P��ֱ��AB�Ϸ�������OP��AB�ڵ�D����![]() �����ֵ��
�����ֵ��
����ͼ3������P��x����Ϸ�������PC����PCΪ����������CPEF�����ŵ�P���˶��������εĴ�С��λ��Ҳ��֮�ı䣮������E��Fǡ������y���ϣ�ֱ��д����Ӧ�ĵ�P�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com