
【题目】近期,某国遭遇了近年来最大的经济危机,导致该国股市大幅震荡,昨天某支股票累计卖出的数量和交易时间之间的关系如图中虚线所示,累计买入的数量和交易时间之间的关系如图中实线所示,其中点A是实线和虚线的交点,点C是BE的中点,CD与横轴平行,则下列关于昨天该股票描述正确的是( )

A.交易时间在3.5h时累计卖出的数量为12万手
B.交易时间在1.4h时累计卖出和累计买入的数量相等
C.累计卖出的数量和累计买入的数量相差1万手的时刻有5个
D.从点A对应的时刻到点C对应的时刻,平均每小时累计卖出的数量小于买入的数量
【答案】D
【解析】
由中点坐标公式可求点C坐标,可得交易时间在3.5h时累计卖出的数量为12.5万手,可判断选项A;利用待定系数法可求AC,OB解析式,可求点B坐标,可得交易时间在1.5h时累计卖出和累计买入的数量相等,可判断选项B;由图象可得累计卖出的数量和累计买入的数量相差1万手的时刻有4个,可判断选项C;由图象可得从点A对应的时刻到点C对应的时刻,实线在虚线的上方,即平均每小时累计卖出的数量小于买入的数量,可判断选项D,即可求解.
∵点B(3,5),点E(4,20),点C是BE的中点,
∴点C(![]() ,
,![]() ),
),
∴交易时间在3.5h时累计卖出的数量为12.5万手,故A选项不合题意;
∵直线OB过点(0,0),点B(3,5),
∴直线OB解析式为:y=![]() x,
x,
∵直线AC过点(1,0),点C(![]() ,
,![]() ),
),
∴直线AC解析式为:y=5x﹣5,
联立方程组可得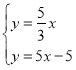 ,
,
∴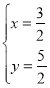
∴交易时间在1.5h时累计卖出和累计买入的数量相等,故B选项不合题意;
由图象可得累计卖出的数量和累计买入的数量相差1万手的时刻有4个,故C选项不合题意,
由图象可得从点A对应的时刻到点C对应的时刻,实线在虚线的上方,即平均每小时累计卖出的数量小于买入的数量,故D选项符合题意,
故选:D.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上,
上,![]() 是直线
是直线![]() 上一点.
上一点.
(1)如图1,若![]() ,点
,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .求证:
.求证:![]() ;
;
(2)如图2,若![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,点
上,点![]() 是
是![]() 上的一个动点(点
上的一个动点(点![]() 与点
与点![]() ,
,![]() 不重合),矩形
不重合),矩形![]() 的顶点
的顶点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上.探究
上.探究![]() 与
与![]() 的关系,并给出证明;
的关系,并给出证明;
(3)在(2)的条件下,当点![]() 满足什么条件时,线段
满足什么条件时,线段![]() 的长最短?(直接给出结论,不必说明理由)
的长最短?(直接给出结论,不必说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 内接于
内接于![]() ,
,![]() 是
是![]() 的直径,过点
的直径,过点![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() ,
,![]() 是
是![]() 上一点,点
上一点,点![]() ,
,![]() 分别位于直径
分别位于直径![]() 异侧,连接
异侧,连接![]() ,
,![]() ,
,![]() ,且
,且![]() .
.
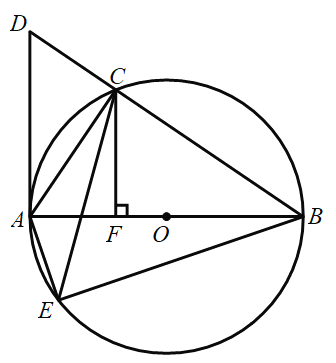
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
材料一:最大公约数是指两个或多个整数共有的约数中最大的一个.我们将两个整数a、b的最大公约数表示为(a,b),如(12,18)=6;(7,9)=1.
材料二:求7x+3y=11的一组整数解,主要分为三个步骤:
第一步,用x表示y,得y![]() ;
;
第二步,找一个整数x,使得11﹣7x是3的倍数,为更容易找到这样的x,将11﹣7x变形为12﹣9x+2x﹣1=3(4﹣3x)+2x﹣1,即只需2x﹣1是3的倍数即可,为此可取x=2;
第三步,将x=2代入y![]() ,得y=﹣1.∴
,得y=﹣1.∴![]() 是原方程的一组整数解.
是原方程的一组整数解.
材料三:若关于x,y的二元一次方程ax+by=c(a,b,c均为整数)有整数解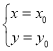 ,则它的所有整数解为
,则它的所有整数解为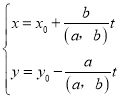 (t为整数).
(t为整数).
利用以上材料,解决下列问题:
(1)求方程(15,20)x+(4,8)y=99的一组整数解;
(2)求方程(15,20)x+(4,8)y=99有几组正整数解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“停课不停学”,某校在线上教学时,要求学生因地制宜开展体育锻炼.为了解学生居家体育锻炼情况,学校对学生四月份平均每天开展体育锻炼的时长情况随机抽取了部分同学进行问卷调查,将调查结果进行了统计分析,并绘制如下两幅不完整的统计图:
(![]() 类:时长
类:时长![]() 分钟;
分钟;![]() 类:
类:![]() 分钟<时长
分钟<时长![]() 分钟;
分钟;![]() 类:
类:![]() 分钟<时长
分钟<时长![]() 分钟;
分钟;![]() 类:
类:![]() 分钟<时长
分钟<时长![]() 分钟;
分钟;![]() 类:时长
类:时长![]() 分钟).
分钟).
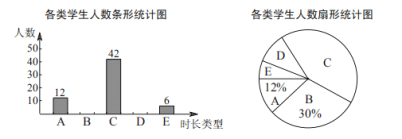
该校共有学生![]() 人,请根据以上统计分析,估计该校四月份平均每天体育锻炼时长超过
人,请根据以上统计分析,估计该校四月份平均每天体育锻炼时长超过![]() 分钟且不超过
分钟且不超过![]() 分钟的学生约有________人.
分钟的学生约有________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
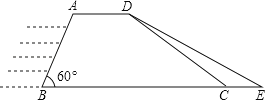
【题目】如图,马边水务部门为加强马边河防汛工作,决定对某水电站水库进行加固.原大坝的横断面是梯形ABCD,如图所示,已知迎水面AB的长为10米,∠B=60°,背水面DC的长度为10![]() 米,加固后大坝的横断面为梯形ABED.若CE的长为4米.
米,加固后大坝的横断面为梯形ABED.若CE的长为4米.
(1)已知需加固的大坝长为120米,求需要填方多少立方米;
(2)求新大坝背水面DE的坡度.(计算结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在直角三角形ABC中,∠ACB=90°,BC的垂直平分线交BC点D,交AB于点E,过点A作AF∥CE交直线DE于点F.
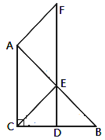
(1)求证:四边形ACEF是平行四边形;
(2)当∠B的大小满足什么条件时,四边形ACEF是菱形?请证明你的结论;
(3)四边形ACEF有可能是矩形吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com