
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,﹣3),点P是直线BC下方抛物线上的任意一点。
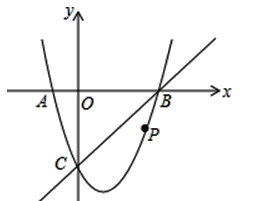
(1)求这个二次函数y=x2+bx+c的解析式。
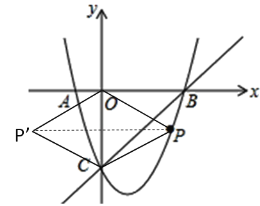
(2)连接PO,PC,并将△POC沿y轴对折,得到四边形POP′C,如果四边形POP′C为菱形,求点P的坐标。
【答案】(1)二次函数的解析式为![]() ;(2)P(
;(2)P(![]() )时,四边形POP′C为菱形.
)时,四边形POP′C为菱形.
【解析】
(1)将点B、C的坐标代入解方程组即可得到函数解析式;
(2)根据四边形POP′C为菱形,得到![]() ,且
,且![]() 与OC互相垂直平分,可知点P的纵坐标为
与OC互相垂直平分,可知点P的纵坐标为![]() ,将点P的纵坐标代入解析式即可得到横坐标,由此得到答案.
,将点P的纵坐标代入解析式即可得到横坐标,由此得到答案.
(1)将点B(3,0)、C(0,﹣3)的坐标代入y=x2+bx+c,得
![]() ,∴
,∴![]()
∴二次函数的解析式为![]() ;
;
(2)如图,
令![]() 中x=0,得y=-3,
中x=0,得y=-3,
∴C(0,-3)
∵四边形POP′C为菱形,
∴![]() ,且
,且![]() 与OC互相垂直平分,
与OC互相垂直平分,
∴点P的纵坐标为![]() ,
,
当y=![]() 时,
时, ![]() ,
,
得: ![]() ,
,
∵点P是直线BC下方抛物线上的任意一点,
∴P(![]() )时,四边形POP′C为菱形.
)时,四边形POP′C为菱形.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与函数
与函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,且点
两点,且点![]() 的坐标为
的坐标为![]() .
.
(1)求![]() 的值;
的值;
(2)已知点![]() ,过点
,过点![]() 作平行于
作平行于![]() 轴的直线,交直线
轴的直线,交直线![]() 于点
于点![]() ,交函数
,交函数![]() 的图象于点
的图象于点![]() .
.
①当![]() 时,求线段
时,求线段![]() 的长;
的长;
②若![]() ,结合函数的图象,直接写出
,结合函数的图象,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以矩形ABCD的边CD为直径作⊙O,点E是AB 的中点,连接CE交⊙O于点F,连接AF并延长交BC于点H.

(1)若连接AO,试判断四边形AECO的形状,并说明理由;
(2)求证:AH是⊙O的切线;
(3)若AB=6,CH=2,则AH的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场一种商品的进价为每件![]() 元,售价为每件
元,售价为每件![]() 元.每天可以销售
元.每天可以销售![]() 件,为尽快减少库存,商场决定降价促销.
件,为尽快减少库存,商场决定降价促销.
(1)若该商品连续两次下调相同的百分率后售价降至每件![]() 元,求两次下降的百分率;
元,求两次下降的百分率;
(2)经调查,若该商品每降价![]() 元,每天可多销售
元,每天可多销售![]() 件,那么每天要想获得最大利润,每件售价应多少元?最大利润是多少?
件,那么每天要想获得最大利润,每件售价应多少元?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC内接于![]() ,点D是
,点D是![]() 的中点,且与点C位于AB的异侧,CD交AB于点E.
的中点,且与点C位于AB的异侧,CD交AB于点E.
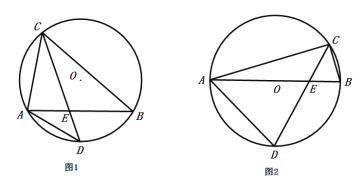
(1)求证:△ADE∽△CDA
(2)如图2,若![]() 的直径AB
的直径AB![]() ,CE=2,求AD和CD的长.
,CE=2,求AD和CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
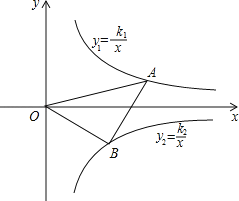
【题目】如图,在平面直角坐标系中,反比例函数y1=![]() (x>0)的图象与y2=
(x>0)的图象与y2=![]() (x>0)的图象关于x轴对称,Rt△AOB的顶点A,B分别在y1=
(x>0)的图象关于x轴对称,Rt△AOB的顶点A,B分别在y1=![]() (x>0)和y2=
(x>0)和y2=![]() (x>0)的图象上.若OB=AB,点B的纵坐标为﹣2,则点A的坐标为_____.
(x>0)的图象上.若OB=AB,点B的纵坐标为﹣2,则点A的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
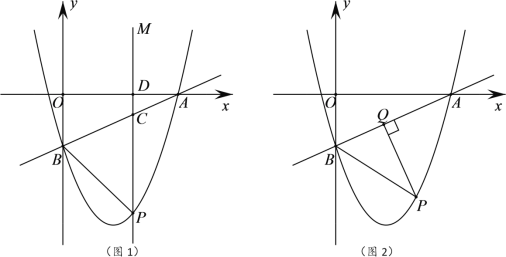
【题目】如图,在平面直角坐标系中,一次函数![]() 的图像分别交x、y轴于点A、B,抛物线
的图像分别交x、y轴于点A、B,抛物线![]() 经过点A、B,点P为第四象限内抛物线上的一个动点.
经过点A、B,点P为第四象限内抛物线上的一个动点.
(1)求此抛物线对应的函数表达式;
(2)如图1所示,过点P作PM∥y轴,分别交直线AB、x轴于点C、D,若以点P、B、C为顶点的三角形与以点A、C、D为顶点的三角形相似,求点P的坐标;
(3)如图2所示,过点P作PQ⊥AB于点Q,连接PB,当△PBQ中有某个角的度数等于∠OAB度数的2倍时,请直接写出点P的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
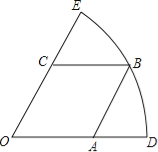
【题目】如图,扇形DOE的半径为3,边长为![]() 的菱形OABC的顶点A,C,B分别在OD,OE,
的菱形OABC的顶点A,C,B分别在OD,OE,![]() 上,若把扇形DOE围成一个圆锥,则此圆锥的高为( )
上,若把扇形DOE围成一个圆锥,则此圆锥的高为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com