
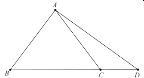
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,延长
,延长![]() 至点
至点![]() ,使
,使![]() ,则
,则![]() ________.
________.
【答案】![]()
【解析】
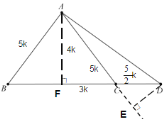
过点A 作AF⊥BC于点,过点D 作DE⊥AC交AC的延长线于点E,目的得到直角三角形利用三角函数得△AFC三边的关系,再证明 △ACF∽△DCE,利用相似三角形性质得出△DCE各边比值,从而得解.
解:过点A 作AF⊥BC于点,过点D 作DE⊥AC交AC的延长线于点E,
∵![]() ,
, ![]()
∴∠B=∠ACF,sin∠ACF=![]() =
=![]() ,
,![]()
设AF=4k,则AC=5k,CD=![]() ,由勾股定理得:FC=3k,
,由勾股定理得:FC=3k,
∵∠ACF=∠DCE,∠AFC=∠DEC=90°,
∴△ACF∽△DCE,
∴AC:CD=CF:CE=AF:DE,即5k: ![]() =3k:CE=4k:DE,
=3k:CE=4k:DE,
解得:CE=![]() ,DE=2k,即AE=AC+CE=5k+
,DE=2k,即AE=AC+CE=5k+![]() =
=![]() ,
,
∴在Rt△AED中,![]() DE:AE=2k:
DE:AE=2k:![]() =
=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA
与⊙O的另一个交点为E,连结AC,CE。

(1)求证:∠B=∠D;
(2)若AB=4,BC-AC=2,求CE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=﹣![]() x+6与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
x+6与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
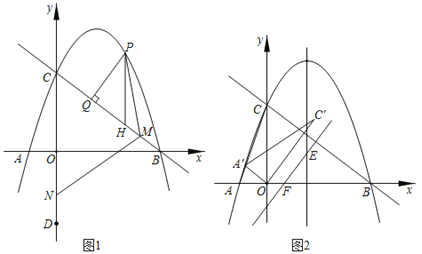
(1)如图1,点P为直线BC上方抛物线上一动点,过点P作PH∥y轴,交直线BC于点H,过点P作PQ⊥BC于点Q,当PQ﹣![]() PH最大时,点C关于x轴的对称点为点D,点M为直线BC上一动点,点N为y轴上一动点,连接PM、MN,求PM+MN+
PH最大时,点C关于x轴的对称点为点D,点M为直线BC上一动点,点N为y轴上一动点,连接PM、MN,求PM+MN+![]() ND的最小值;
ND的最小值;
(2)如图2,连接AC,将△OAC绕着点O顺时针旋转,记旋转过程中的△OAC为△OA'C',点A的对应点为点A',点C的对应点为点C'.当点A'刚好落在线段AC上时,将△OA'C'沿着直线BC平移,在平移过程中,直线OC'与抛物线对称轴交于点E,与x轴交于点F,设点R是平面内任意一点,是否存在点R,使得以B、E、F、R为顶点的四边形是菱形?若存在,请直接写出点R的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与双曲线
与双曲线![]() 在第一象限内交于
在第一象限内交于![]() 、
、![]() 两点,已知
两点,已知![]() ,
,![]() .
.

(1)![]() __________,
__________,![]() ____________________,
____________________,![]() ____________________.
____________________.
(2)直接写出不等式![]() 的解集;
的解集;
(3)设点![]() 是线段
是线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() 是
是![]() 轴上一点,求
轴上一点,求![]() 的面积
的面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,﹣3),点P是直线BC下方抛物线上的任意一点。
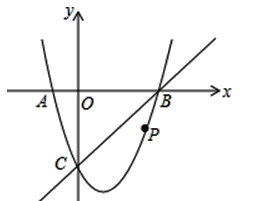
(1)求这个二次函数y=x2+bx+c的解析式。
(2)连接PO,PC,并将△POC沿y轴对折,得到四边形POP′C,如果四边形POP′C为菱形,求点P的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:三角形一边上的点将该边分为两条线段,且这两条线段的积等于这个点到该边所对顶点连线的平方,则称这个点为三角形该边的“好点”.如图1,△ABC中,点D是BC边上一点,连结AD,若![]() ,则称点D是△ABC中BC边上的“好点”.
,则称点D是△ABC中BC边上的“好点”.
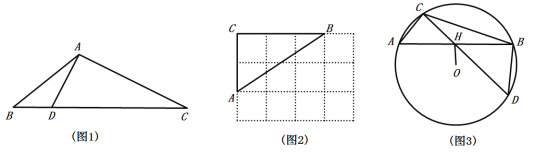
(1)如图2,△ABC的顶点是![]() 网格图的格点,请仅用直尺画出AB边上的一个“好点”.
网格图的格点,请仅用直尺画出AB边上的一个“好点”.
(2)△ABC中,BC=9,![]() ,
,![]() ,点D是BC边上的“好点”,求线段BD的长.
,点D是BC边上的“好点”,求线段BD的长.
(3)如图3,△ABC是![]() 的内接三角形,OH⊥AB于点H,连结CH并延长交
的内接三角形,OH⊥AB于点H,连结CH并延长交![]() 于点D.
于点D.
①求证:点H是△BCD中CD边上的“好点”.
②若![]() 的半径为9,∠ABD=90°,OH=6,请直接写出
的半径为9,∠ABD=90°,OH=6,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝中华人民共和国建国70周年,某校从A、B两位男生和D、E两位女生中选派学生,参加全区中小学“我和我的祖国”演讲比赛.
(1)如果选派一位学生参赛,那么选派到的代表是A同学的概率是 ;
(2)如果选派两位学生参赛,用树状图或列表法,求恰好选派一男一女两位同学参赛的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李在景区销售一种旅游纪念品,已知每件进价为6元,当销售单价定为8元时,每天可以销售200件.市场调查反映:销售单价每提高1元,日销量将会减少10件,物价部门规定:销售单价不能超过12元,设该纪念品的销售单价为x(元),日销量为y(件),日销售利润为w(元).
(1)求y与x的函数关系式.
(2)要使日销售利润为720元,销售单价应定为多少元?
(3)求日销售利润w(元)与销售单价x(元)的函数关系式,当x为何值时,日销售利润最大,并求出最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com