
【题目】已知:函数y=﹣x2+mx+2m(m为常数)的图象不经过第二象限,当﹣5≤x≤1时,函数的最大值与最小值之差为12.25,则m的值为_____.
【答案】-3或-5
【解析】
由题意可知m≤0,当![]() ≤0时,△≤0,则﹣8≤m≤0,函数的最大值为
≤0时,△≤0,则﹣8≤m≤0,函数的最大值为![]() +2m,函数的最小值为3m﹣1,据此结合已知进行求解即可得.
+2m,函数的最小值为3m﹣1,据此结合已知进行求解即可得.
∵函数y=﹣x2+mx+2m(m为常数)的图象不经过第二象限,-1<0,
∴函数图象开口向下,与y轴交于原点或负半轴,
∴2m≤0,此时△≤0,
∴m≤0,
∵抛物线的对称轴x=![]() ,
,
∴![]() ≤0,
≤0,
即对称轴在y轴或y轴左侧,
∴抛物线与x轴的交点又一个或没有交点,
∴△=m2+8m≤0,
∴﹣8≤m≤0,
∴-4≤![]() ≤0,
≤0,
∴当﹣5≤x≤1时,
函数在x=![]() 时取最大值为
时取最大值为![]() +2m,
+2m,
x=-5时,y=-25-3m,
x=1时,y=3m-1,
∵-25-3m-(3m-1)=-24-6m,
∴当﹣8≤m<-4时,-25-3m-(3m-1)=-24-6m>0,
当﹣4≤m≤0时,-25-3m-(3m-1)=-24-6m≤0,
∴①当﹣8≤m<-4时, 3m-1为最小值,
则有![]() +2m﹣3m+1=12.25,
+2m﹣3m+1=12.25,
∴m=﹣5或m=9(舍去);
②当﹣4≤m≤0时,-25-3m为最小值,
则有![]() +2m-(-25-3m)=12.25,
+2m-(-25-3m)=12.25,
∴m=-3或m=-17(舍去),
综上,m=-3或m=-5,
故答案为:-3或-5.


科目:初中数学 来源: 题型:
【题目】如图1,分别沿长方形纸片ABCD和正方形纸片EFGH的对角线AC,EG剪开,拼成如图2所示的ALMN,若中间空白部分四边形OPQR恰好是正方形,且ALMN的面积为50,则正方形EFGH的面积为( )
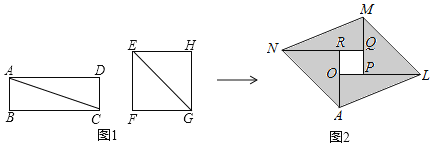
A. 24 B. 25 C. 26 D. 27
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,AD=3,点E是边CD的中点,点P,Q分别是射线DC与射线EB上的动点,连结PQ,AP,BP,设DP=t,EQ=![]() t.
t.
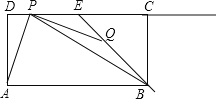
(1)当点P在线段DE上(不包括端点)时.
①求证:AP=PQ;②当AP平分∠DPB时,求△PBQ的面积.
(2)在点P,Q的运动过程中,是否存在这样的t,使得△PBQ为等腰三角形?若存在,请求出t的值;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,⊙O的半径为r(r>0).给出如下定义:若平面上一点P到圆心O的距离d,满足![]() ,则称点P为⊙O的“随心点”.
,则称点P为⊙O的“随心点”.
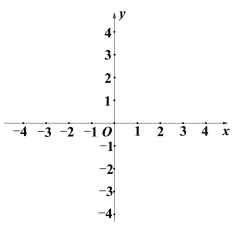
(1)当⊙O的半径r=2时,A(3,0),B(0,4),C(![]() ,2),D(
,2),D(![]() ,
,![]() )中,⊙O的“随心点”是 ;
)中,⊙O的“随心点”是 ;
(2)若点E(4,3)是⊙O的“随心点”,求⊙O的半径r的取值范围;
(3)当⊙O的半径r=2时,直线y=- x+b(b≠0)与x轴交于点M,与y轴交于点N,若线段MN上存在⊙O的“随心点”,直接写出b的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
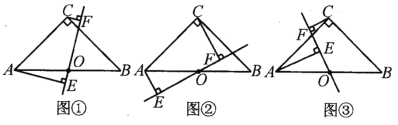
【题目】如图,在△ABC中,∠ACB=90,∠ABC=45 ,点O是AB的中点,过A、C两点向经过点O的直线作垂线,垂足分别为E、F.
(1)如图①,求证:EF=AE+CF.
(2)如图②,图③,线段EF、AE、CF之间又有怎样的数量关系?请直接写出你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司对自家办公大楼一块![]() 米的正方形墙面进行了如图所示的设计装修(四周阴影部分是八个全等的矩形,用材料甲装修;中心区是正方形
米的正方形墙面进行了如图所示的设计装修(四周阴影部分是八个全等的矩形,用材料甲装修;中心区是正方形![]() ,用材料乙装修). 两种材料的成本如下表:
,用材料乙装修). 两种材料的成本如下表:

材料 | 甲 | 乙 |
价格(元/米2) | 550 | 500 |
设矩形的较短边![]() 的长为
的长为![]() 米,装修材料的总费用为
米,装修材料的总费用为![]() 元.
元.
(1)计算中心区的边![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(2)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)当中心区的边长![]() 不小于2米时,预备材料的购买资金32000元够用吗?请利用函数的增减性来说明理由.
不小于2米时,预备材料的购买资金32000元够用吗?请利用函数的增减性来说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是BC边上的一点,BE=4,EC=8,将正方形边AB沿AE折叠到AF,延长EF交DC于G,连接AG,现在有如下四个结论:①∠EAG=45°;②FG=FC;③FC∥AG;④S△GFC=14.其中结论正确的序号是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
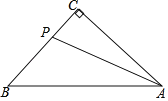
【题目】如图,在等腰Rt△ABC中,∠ACB=90°,AC=BC,点P为BC边上一点(不与B、C重合),连接PA,以P为旋转中心,将线段PA顺时针旋转90°,得到线段PD,连接DB.
(1)请在图中补全图形;
(2)∠DBA的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A、B、C是直径为6cm的⊙O上的点,且AB=3cm,AC=3![]() cm,则∠BAC的度数为( )
cm,则∠BAC的度数为( )
A. 15° B. 75°或15° C. 105°或15° D. 75°或105°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com