
【题目】在平面直角坐标系xOy中,抛物线![]() 与x轴交于点A,B(A在B的左侧),抛物线的对称轴与x轴交于点D,且OB=2OD.
与x轴交于点A,B(A在B的左侧),抛物线的对称轴与x轴交于点D,且OB=2OD.
(1)当![]() 时,
时,
①写出抛物线的对称轴;
②求抛物线的表达式;
(2)存在垂直于x轴的直线分别与直线![]() :
:![]() 和抛物线交于点P,Q,且点P,Q均在x轴下方,结合函数图象,求b的取值范围.
和抛物线交于点P,Q,且点P,Q均在x轴下方,结合函数图象,求b的取值范围.
【答案】(1)①![]() ;②
;②![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)①由二次函数的对称轴方程可得出答案;
②根据题意求出B点坐标为(2,0),代入抛物线解析式![]() 可得出答案;
可得出答案;
(2)求出E(-![]() ,0),点D的坐标为(-
,0),点D的坐标为(-![]() ,0).①当b>0时,得出点A的坐标为(-2b,0),点B的坐标为(b,0),则-2b<-
,0).①当b>0时,得出点A的坐标为(-2b,0),点B的坐标为(b,0),则-2b<-![]() ,解不等式即可;②当b<0时,点A的坐标为(0,0),点B的坐标为(-b,0),则0<-
,解不等式即可;②当b<0时,点A的坐标为(0,0),点B的坐标为(-b,0),则0<-![]() ,解出b<-2.
,解出b<-2.
解:(1)当![]() 时,
时,![]() 化为
化为![]() .
.
①![]() .
.
②∵抛物线的对称轴为直线![]() ,
,
∴点D的坐标为(-1,![]() ),OD=1.
),OD=1.
∵OB=2OD,
∴ OB=2.
∵点A,点B关于直线![]() 对称,
对称,
∴点B在点D的右侧.
∴ 点B的坐标为(![]() ,
,![]() ).
).
∵抛物线![]() 与x轴交于点B(
与x轴交于点B(![]() ,
,![]() ),
),
∴ ![]() .
.
解得![]() .
.
∴抛物线的表达式为![]() .
.
(2)设直线![]() 与x轴交点为点E,
与x轴交点为点E,
当y=0时,![]()
∴ ![]()
∴ E(![]() ,0).
,0).
抛物线的对称轴为![]() ,
,
∴点D的坐标为(![]() ,
,![]() ).
).
①当![]() 时,
时,![]() .
.
∵OB=2OD,
∴ OB=b.
∴ 点A的坐标为(![]() ,
,![]() ),点B的坐标为(b,
),点B的坐标为(b,![]() ).
).
当![]() <
<![]() 时,存在垂直于x轴的直线分别与直线
时,存在垂直于x轴的直线分别与直线![]() :
:![]() 和抛物线交于点P,Q,且点P,Q均在x轴下方,
和抛物线交于点P,Q,且点P,Q均在x轴下方,

解得![]() .
.
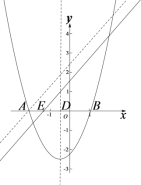
②当![]() 时,
时,![]() .
.
∴ ![]() .
.
∵OB=2OD,
∴ OB=-b.
∵抛物线![]() 与x轴交于点A,B,且A在B的左侧,
与x轴交于点A,B,且A在B的左侧,
∴ 点A的坐标为(![]() ,
,![]() ),点B的坐标为(-b,
),点B的坐标为(-b,![]() ).
).
当0<![]() 时,存在垂直于x轴的直线分别与直线
时,存在垂直于x轴的直线分别与直线![]() :
:![]() 和抛物线交于点P,Q,且点P,Q均在x轴下方,
和抛物线交于点P,Q,且点P,Q均在x轴下方,
解得b<-2.
综上,b的取值范围是![]() 或
或![]() .
.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】有两个旅游公司经营某景点的门票销售.甲公司只经营散客门票,票价为40元∕张;乙公司只经营团体票,一次购买门票不超过10张,票价为50元∕张,一次性购买门票超过10张时,其中有10张门票的票价仍为50元∕张,超出10张部分的票价为30元∕张.某班部分同学要去该景点旅游,设参加旅游的学生有![]() 人(
人(![]() 为非负整数).
为非负整数).
(1)根据题意填表:
一次购买门票数量∕张 |
|
|
| … |
甲旅游公司费用∕元 |
| … | ||
乙旅游公司费用∕元 |
| … |
(2)设去甲旅游公司购买门票费用为![]() 元,去乙旅游公司购买门票费用为
元,去乙旅游公司购买门票费用为![]() 元,分别求
元,分别求![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)根据题意填空:
①若在甲公司和在乙公司购买门票的数量相同,且费用相同,则在同一个旅游公司一次购买门票的数量为 张;
②若在同一个旅游公司一次购买门票![]() 张,则在甲、乙两个旅游公司中的 公司购买花费少;
张,则在甲、乙两个旅游公司中的 公司购买花费少;
③若在同一个旅游公司一次购买门票花费了![]() 元,则在甲、乙两个旅游公司中 公司购买门票数量多.
元,则在甲、乙两个旅游公司中 公司购买门票数量多.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 与x轴交于点A,B(A在B的左侧),抛物线的对称轴与x轴交于点D,且OB=2OD.
与x轴交于点A,B(A在B的左侧),抛物线的对称轴与x轴交于点D,且OB=2OD.
(1)当![]() 时,
时,
①写出抛物线的对称轴;
②求抛物线的表达式;
(2)存在垂直于x轴的直线分别与直线![]() :
:![]() 和抛物线交于点P,Q,且点P,Q均在x轴下方,结合函数图象,求b的取值范围.
和抛物线交于点P,Q,且点P,Q均在x轴下方,结合函数图象,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB = 90,D为AB的中点,AE∥DC,CE∥DA.
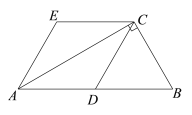
(1)求证:四边形ADCE是菱形;
(2)连接DE,若AC =![]() ,BC =2,求证:△ADE是等边三角形.
,BC =2,求证:△ADE是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A:篮球 B:乒乓球C:羽毛球 D:足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:


(1)这次被调查的学生共有 人;
(2)请你将条形统计图(2)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年疫情期间,为防止疫惰扩散,人们见面的机会少了,但是随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷.为此,李老师设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),进行调查.将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次参与调查的共有_______人:在扇形统计图中,表示“微信”的扇形圆心角的度数为_______;其它沟通方式所占的百分比为_______;
(2)将条形统计图补充完整;
(3)如果我国有13亿人在使用手机.①请估计最喜欢用“微信”进行沟通的人数:并:用科学计数法表示;②在全国使用手机的人中随机抽取一人,用频率估计概率,求抽取的恰好使用“QQ”的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
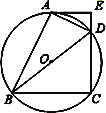
【题目】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD交CD的延长线于点E,DA平分∠BDE.
⑴求证:AE是⊙O的切线;
⑵若AE=4cm,CD=6cm,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com