
已知反比例函数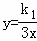 的图象与一次函数y=k2x+m的图象交于A(﹣1,a)、B(
的图象与一次函数y=k2x+m的图象交于A(﹣1,a)、B(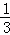 ,﹣3)两点,连结AO.
,﹣3)两点,连结AO.
(1)求反比例函数和一次函数的表达式;
(2)设点C在y轴上,且与点A、O构成等腰三角形,请直接写出点C的坐标.

考点: 反比例函数与一次函数的交点问题.
分析: (1)将点A(﹣1,a)、B(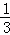 ,﹣3)代入反比例函数
,﹣3)代入反比例函数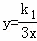 中得:﹣3×
中得:﹣3×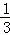 =(﹣1)×a=k1,可求k1、a;再将点A(﹣1,a)、B(
=(﹣1)×a=k1,可求k1、a;再将点A(﹣1,a)、B(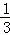 ,﹣3)代入y2=k2x+m中,列方程组求k2、m即可;
,﹣3)代入y2=k2x+m中,列方程组求k2、m即可;
(2)分三种情况:①OA=OC;②AO=AC;③CA=CO;讨论可得点C的坐标.
解答: 解:(1)∵反比例函数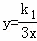 的图象经过B(
的图象经过B(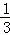 ,﹣3),
,﹣3),
∴k1=3×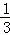 ×(﹣3)=﹣3,
×(﹣3)=﹣3,
∵反比例函数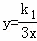 的图象经过点A(﹣1,a),
的图象经过点A(﹣1,a),
∴a=1.
由直线y2=k2x+m过点A,B得:
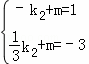 ,
,
解得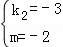 .
.
∴反比例函数关系式为y=﹣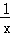 ,一次函数关系式为y=﹣3x﹣2;
,一次函数关系式为y=﹣3x﹣2;
(2)点C在y轴上,且与点A、O构成等腰三角形,点C的坐标为:(0,﹣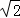 )或(0,
)或(0,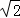 )或(0,2)或(0,1).
)或(0,2)或(0,1).
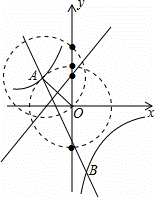
如图,线段OA的垂直平分线与y轴的交点,有1个;
以点A为圆心、AO长为半径的圆与y轴的交点,有1个;
以点O为圆心、OA长为半径的圆与y轴的交点,有2个.
以上四个点为所求.
点评: 此题综合考查了待定系数法求函数解析式的方法、等腰三角形的性质等知识,注意分类思想的运用.


科目:初中数学 来源: 题型:
.某中学准备建一个面积为375m2的矩形游泳池,且游泳池的周长为80m.设游泳池的长为xm,则可列方程( )
A. x(80﹣x)=375 B. x(80+x)=375 C. x(40﹣x)=375 D. x(40+x)=375
查看答案和解析>>
科目:初中数学 来源: 题型:
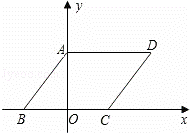
如图,▱ABCD在平面直角坐标系中,AD=6,若OA、OB的长是关于x的一元二次方程x2﹣7x+12=0的两个根,且OA>OB.
(1)求sin∠ABC的值;
(2)若E为x轴上的点,且S△AOE=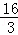 ,求经过D、E两点的直线的解析式,并判断△AOE与△DAO是否相似?
,求经过D、E两点的直线的解析式,并判断△AOE与△DAO是否相似?
(3)若点M在平面直角坐标系内,则在直线AB上是否存在点F,使以A、C、F、M为顶点的四边形为菱形?若存在,请直接写出F点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
从某玉米种子中抽取6批,在同一条件下进行发芽试验,有关数据如下:
种子粒数 100 400 800 1000 2000 5000
发芽种子粒数 85 298 652 793 1604 4005
发芽频率 0.850 0.745 0.815 0.793 0.802 0.801
根据以上数据可以估计,该玉米种子发芽的概率约为 (精确到0.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
数轴上表示整数的点称为整点.某数轴的单位长度是1厘米,若在这个数轴上随意画出一条长为2009厘米的线段AB,则线段AB盖住的整点的个数是( )
A. 2007或2008 B. 2008或2009 C. 2009或2010 D. 2010或2011
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com