
已知:二次函数y=ax2+bx+6(a≠0)的图象与x轴交于A 、B两点(点A在点B的左侧),点A、点B的横坐标是方程x2-4x-12=0的两个根.
、B两点(点A在点B的左侧),点A、点B的横坐标是方程x2-4x-12=0的两个根.
(1)求出该二次函数的表达式及顶点坐标;
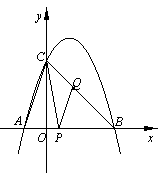
(2)如图,连接AC、BC,点P是线段OB上一个动点(点P不与点O、B重合),过点P作PQ∥AC交BC于点Q,当△CPQ的面积最大时,求点P的坐标.
 |
(1)由x2-4x-12=0,x=-2或 x=6…………………………………(1分)
x=6…………………………………(1分)
故A(-2,0)、B(6,0)、C(0,6). 二次函数y=a (x2-4x-12)中,-12a=6
∴a=-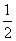 ,故二次函数y=-
,故二次函数y=-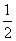 x2+2x+6,顶点坐标(2,8)………………… (3分)
x2+2x+6,顶点坐标(2,8)………………… (3分)
(2)设点P的横坐标为m,则0<m<6…………………………………………………(4分)
连结AQ,由PQ∥AC,知S△CPQ=S△APQ=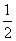 (m+2)·
(m+2)·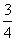 (6-m) ……………………(6分)
(6-m) ……………………(6分)
=- ( m2-4m-12)=-
( m2-4m-12)=- (m-2)2+6,当m=2时,S最大=6……………………(7分)
(m-2)2+6,当m=2时,S最大=6……………………(7分)
所以,当△CPQ的面积最大时,点P的坐标是(2,0)…………………………(8分)


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
股票每天的涨、跌幅均不能超过10%,即当涨了原价的10%后,便不能再涨,叫做涨停;当跌了原价的10%后,便不能再跌,叫做跌停.已知一支股票某天跌停,之后两天时间又涨回到原价,若这两天此股票股价的平均增长率为x,则x满足的方程是( )
A. =
= B.
B. =
= C.1+2x=
C.1+2x= D.1+2x=
D.1+2x=
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△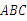 中,∠
中,∠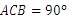 ,
,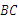 的垂直平分线
的垂直平分线 交
交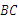 于点
于点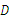 ,交
,交 于点
于点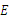 ,点
,点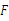 在
在 上,且
上,且 .
.
(1)求证:四边形 是平行四边形.
是平行四边形.
(2)当∠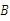 满足什么条件时,四边形
满足什么条件时,四边形 是菱形?并说明理由.
是菱形?并说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
在一个不透明的布袋里装有4个完全相同的标有数字1、2、3、4的小球. 小明从布袋里随机取出一个小球,记下数字为x,小红从布袋里剩下的小球中随机取出一个 ,记下数字为y. 计算由x、y确定的点(x,y)在函数y=-x+5的图象上的概率.
,记下数字为y. 计算由x、y确定的点(x,y)在函数y=-x+5的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
数学活动课上,老师提出这样一个问题:如果AB=BC,∠ABC=60°,∠APC=30°,连接
PB,那么PA、PB、PC之间会有怎样的等量关系呢?
经过思考后,部分同学进行了如下的交流:
小蕾:我将图形进行了特殊化,让点P在BA延长线上(如图1),得到了一个猜想:
PA2+PC2=PB2 .
小东:我假设点P在∠ABC的内部,根据题目条件,这个图形具有“共端点等线段”的特点,可以利用旋转解决问题,旋转△PAB 后得到△P′CB ,并且可推出△PBP′ ,△PCP′ 分别是等边三角形、直角三角形,就能得到猜想和证明方法.
这时老师对同学们说,请大家完成以下问题:
(1)如图2,点P在∠ABC的内部,
①PA=4,PC= ,PB= .
,PB= .
②用等式表示PA、PB、PC之间的数量关系,并证明.
 (2)对于点P的其他位置,是否始终具有②中的结论?若是,请证明;若不是,请举例说明.
(2)对于点P的其他位置,是否始终具有②中的结论?若是,请证明;若不是,请举例说明.
|
|

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com