
【题目】如图所示,将△ABC沿直线BC方向平移△DEF的位置,G是DE上一点,连接AG,过点A、D作直线MN. 
(1)求证:∠AGE=∠GAD+∠ABC;
(2)若EDF=∠DAG,∠CAG+∠CEG=180°,判断AG与DE的位置关系,并证明你的结论.
【答案】
(1)解:由平移的性质得:△ABC≌△DEF,
∴AB=DE,AB∥DE,
∴四边形ABED为平行四边形,
∴AD∥BF,∠ADG=∠ABC,
∴∠ADG=∠DEF,
∴∠ABC=∠DEF=∠ADG,
∵∠AGE为△ADG的外角,
∴∠AGE=∠DAG+∠ADG=∠GAD+∠ABC
(2)解:AG⊥DE,理由为:
由平移的性质得到∠EDF=∠BAC,
∵∠EDF=∠DAG,
∴∠BAC=∠DAG,
∵AB∥DE,
∴∠ABC+∠BEG=180°,
∵∠CAG+∠CEG=180°,
∴∠ABC=∠CAG,
∵MN∥BC,∴∠ABC=∠MAB,
∴∠MAB=∠CAG,
∵∠MAB+∠BAC+∠CAG+∠DAG=180°,
∴∠CAG+∠BAC=90°,即∠BAG=90°,
∵AB∥DE,
∴∠BAG+∠AGD=90°,
则AG⊥DE.
【解析】(1)利用平移的性质得到AB与DE平行且相等,得到四边形ABED为平行四边形,利用平行四边形的性质得到对角相等,利用外角性质即可得证;(2)AG垂直与DE,理由为:由平移的性质得到∠EDF=∠BAC,根据∠EDF=∠DAG,等量代换得到∠BAC=∠DAG,由AB与DE平行,利用两直线平行同旁内角互补得到一对角互补,等量代换得到∠ABC=∠CAG,利用等式的性质及平行线的性质即可得证.
【考点精析】解答此题的关键在于理解平行线的判定与性质的相关知识,掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质,以及对多边形内角与外角的理解,了解多边形的内角和定理:n边形的内角和等于(n-2)180°.多边形的外角和定理:任意多边形的外角和等于360°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】过线段MN的中点画直线l⊥MN,若MN=5 cm,则点M到直线l的距离为( )
A. 5 cm B. 2.5 cm C. 10 cm D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑,每台电子白板各多少万元?
(2)根据学校实际,需至少购进电脑和电子白板共30台,总费用不超过28万元,那么电子白板最多能买几台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过平行四边形ABCD对角线交点O的直线交AD于E,交BC于F,若AB=5,BC=6,OE=2,那么四边形EFCD周长是( )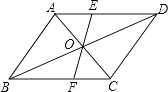
A.16
B.15
C.14
D.13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人体中红细胞的直径约为0.000 007 7 m,这个数用科学记数法表示为( )
A. 77×10-7B. 7.7×10-7C. 0.77×10-5D. 7.7×10-6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,回答问题:
(1)在化简 ![]() 的过程中,小张和小李的化简结果不同;
的过程中,小张和小李的化简结果不同;
小张的化简如下: ![]() =
= ![]() =
= ![]() =
= ![]() ﹣
﹣ ![]()
小李的化简如下: ![]() =
= ![]() =
= ![]() =
= ![]() ﹣
﹣ ![]()
请判断谁的化简结果是正确的,谁的化简结果是错误的,并说明理由.
(2)请你利用上面所学的方法化简 ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com