练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

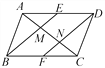
    【题目】如图，在平行四边形ABCD中，E，F分别是边AD，BC的中点，AC分别交BE，DF于点M，N，给出下列结论：①△ABM≌△CDN；②AM＝AC；③DN＝2NF；④S△AMB＝S△ABC，其中正确的结论是__ __．(填序号)

    【答案】①②③

    【解析】在ABCD中，AD∥BC，AD=BC，

    又E、F分别是边AD、BC的中点，

    ∴BF∥DE，BF=DE，

    ∴四边形BFDE是平行四边形，

    ∴BE∥DF，

    ∴∠AMB=∠ANF=∠DNC，

    ∵∠BAM=∠DCN，AB=CD，

    ∴△ABM≌△CDN；

    E是AD的中点，BE∥DF，

    ∴M是AN的中点，

    同理N是CM的中点，

    ∴AM="1/3" AC；

    DN=BM=2NF；

    S△AMB=1/2S△ABC不成立．故答案为：①②③．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在一个不透明的口袋中装有9个黄球，13个黑球，11个红球，它们除颜色外其余都相同.

    (1)求从袋中摸出一个球是红球的概率；

    (2)现从袋中取出若干个黄球，井放入相同数量的黑球，若要使搅拌均与后从袋中摸出一个球是黑球的概率不小于，问至少要取出多少个黄球?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，E、F是平行四边形ABCD对角线AC上两点，AE=CF．

    证明（1）△ABE≌△CDF；

    （2）BE∥DF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，平面直角坐标系中，点A、B分别在x、y轴上，点B的坐标为（0，1），∠BAO=30°．

    （1）求AB的长度；

    （2）以AB为一边作等边△ABE，作OA的垂直平分线MN交AB的垂线AD于点D．求证：BD=OE；

    （3）在（2）的条件下，连接DE交AB于F．求证：F为DE的中点．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某环保小组为了解世博园的游客在园区内购买瓶装饮料数量的情况，一天，他们分别在A、B、C三个出口处，对离开园区的游客进行调查，其中在A出口调查所得的数据整理后绘成如下图所示统计图：

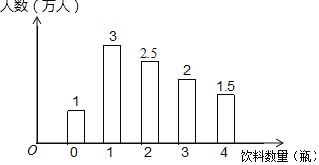
    （1）在A出口的被调查游客中，购买瓶装饮料的数量的中位数是______瓶、众数是______瓶、平均数是______瓶；

    （2）已知A、B、C三个出口的游客量比为2：2：1，用上面图表的人均购买饮料数量计算：这一天景区内若有50万游客，那么这一天购买的饮料的总数是多少？

    表一：

    出口

    B

    C

    人均购买饮料数量（瓶）

    3

    2

    （3）若每瓶饮料要消耗0.5元处理包装的环保费用，该日需要花费多少钱处理这些饮料瓶？由此请你对游客做一点环保宣传建议．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一农民带上若干千克自产的土豆进城出售，为了方便，他带了一些零钱备用，按市场价售出一些后，又降价出售，他手中持有的钱数（含备用零钱）y与售出的土豆千克数x的关系如图所示，结合图象回答下列问题：

    （1）农民自带的零钱是______元，降价前他每千克土豆出售的价格是______元；

    （2）降价后他按每千克0.8元将剩余土豆售完，这时他手中的钱（含备用零钱）是62元，求降价后的线段所表示的函数表达式并写出它的取值范围．

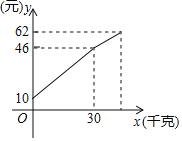
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，四边形ABCD中，AB∥CD，∠B=90°，AC=AD．动点P从点B出发沿折线B-A-D-C方向以1单位/秒的速度运动，在整个运动过程中，△BCP的面积S与运动时间t（秒）的函数图象如图2所示，则AD等于（　　）

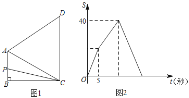
    A. 10B. C. 8D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

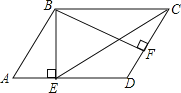
    【题目】在平行四边形ABCD中，BE⊥AD于点E，BF⊥CD于点F，若∠EBF=60°，且AE=2，DF=1，则EC的长为_____________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（本题满分6分）一只不透明的袋子中装有1个白球、1个蓝球和2个红球，这些球除颜色外都相同．

    （1）从袋中随机摸出1个球，摸出红球的概率为 ；

    （2）从袋中随机摸出1个球（不放回）后，再从袋中余下的3个球中随机摸出1个球，球两次摸到的球颜色不相同的概率．

    查看答案和解析>>

    同步练习册答案