
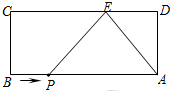
 如图,长方形ABCD中,AB=9,AD=4.E为CD边上一点,CE=6.
如图,长方形ABCD中,AB=9,AD=4.E为CD边上一点,CE=6.分析 (1)由长方形ABCD中,AB=9,CE=6,可求得DE的长,又由AD=4,利用勾股定理即可求得AE的长;
(2)①首先利用勾股定理,可求得CP=$\sqrt{B{C}^{2}+C{P}^{2}}$=$\sqrt{16{+t}^{2}}$,又由CP=AE,可得方程$\sqrt{16+{t}^{2}}$=5,继而求得答案;
②分别从AE=AP与AE=PE去分析求解即可求得答案.
解答 解:(1)∵四边形ABCD是长方形,
∴CD=AB=9,BC=AD=4,∠D=90°,
∵CE=6,
∴DE=CD-CE=3,
∴AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=5;
(2)①根据题意得:BP=t,
∴CP=$\sqrt{B{C}^{2}+C{P}^{2}}$=$\sqrt{16{+t}^{2}}$,
∵CP=AE,
∴$\sqrt{16+{t}^{2}}$=5,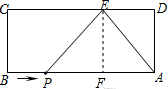
解得:t=3;
②若AP=AE=5,
∴BP=AB-AP=9-5=4,
∴t=4;
若PE=AE=5,则过点E作EF⊥AB于点F,
则四边形ADEF是矩形,
∴PF=AF=DE=3,
∴AP=AF+PF=6,
∴t=BP=AB-AP=3.
综上所述,当t=3或t=4时,△PAE是以AE为腰的等腰三角形.
点评 此题考查了矩形的性质、勾股定理以及等腰三角形的性质.注意掌握辅助线的作法,注意掌握分类讨论思想与方程思想的应用是解此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
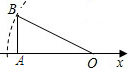 如图,在Rt△OAB中OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,斜边OB的长为半径画弧,交负半轴于一点,则这个点表示的实数是( )
如图,在Rt△OAB中OA长为2,边AB长为1,OA在数轴上,以原点O为圆心,斜边OB的长为半径画弧,交负半轴于一点,则这个点表示的实数是( )| A. | $\sqrt{5}$ | B. | -$\sqrt{5}$ | C. | -2 | D. | -$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,现有一圆心角为90°、半径为80cm的扇形铁片,用它恰好围成一个圆锥形的量筒;如果用其它铁片再做一个圆形盖子把量筒底面密封.(接缝都忽略不计).
如图所示,现有一圆心角为90°、半径为80cm的扇形铁片,用它恰好围成一个圆锥形的量筒;如果用其它铁片再做一个圆形盖子把量筒底面密封.(接缝都忽略不计).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
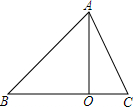 如图,在△ABC中,AO⊥BC,垂足为O,若AO=3,∠B=45°,△ABC的面积为6,则AC边长的平方的值是( )
如图,在△ABC中,AO⊥BC,垂足为O,若AO=3,∠B=45°,△ABC的面积为6,则AC边长的平方的值是( )| A. | 10 | B. | 8 | C. | 6 | D. | 18 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
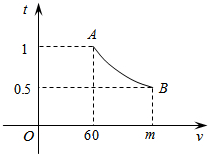 一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:t=$\frac{k}{v}$其图象为如图所示的一段曲线且端点为A(60,1),和B(m,0.5)
一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:t=$\frac{k}{v}$其图象为如图所示的一段曲线且端点为A(60,1),和B(m,0.5)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
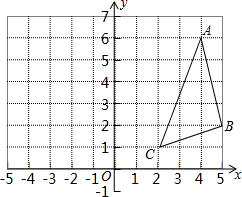 如图,△ABC的顶点坐标分别为A(4,6),B(5,2),C(2,1),
如图,△ABC的顶点坐标分别为A(4,6),B(5,2),C(2,1),查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com