练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    为保证中、小学生每天锻炼一小时，某校开展了形式多样的体育活动项目，小明对某班同学参加锻炼的情况进行了统计，并绘制了下面的统计图①和图②．(1)请根据所给信息在图①中将表示“乒乓球”项目的图形补充完整；（2）扇形统计图②中表示“足球”项目扇形的扇形圆心角的度数是 ．（3）该校中小学生共有2000名．请估计该校共有多少名同学参加“其他”项目的体育活动．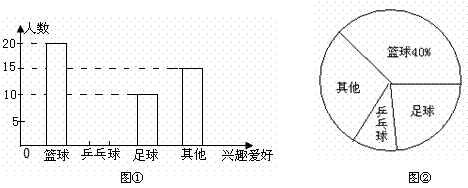


    解：（1）图略    ……………2分                  （2）72°………………4分

    （3）×2000＝600（人）………………………………………………………7分

    答：该校约有600名同学参加“其他”项目的体育活动．…………………………8分


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    函数y＝的自变量x的取值范围是_______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


        图①为某体育场100 m比赛终点计时台侧面示意图，已知：AB＝1m，DE＝5 m，BC⊥DC，∠ADC＝30°，∠BEC＝60°．

        (1)求AD的长度；（结果保留根号）

    (2)如图②，为了避免计时台AB和AD的位置受到与水平面成45°角的光线照射，计时台上方应放直径是多少米的遮阳伞？（精确到0.1 m，参考数据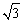：≈1.73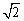，≈1.41）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    分解因式y2－2y＋1＝    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    2－1＋()－       

    查看答案和解析>>

    科目：初中数学 来源： 题型：


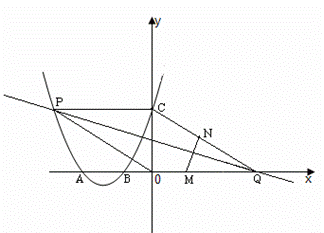
    如图，二次函数的图象与x轴相交于点A(－3，0)、B(－1，0)，与y轴相交于点C(0，3)，点P是该图象上的动点；一次函数y＝kx－4k(k≠0)的图象过点P交x轴于点Q．

    （1）求该二次函数的解析式；

    （2）当点P的坐标为(－4，m)时，求证：∠OPC＝∠AQC；

    （3）点M、N分别在线段AQ、CQ上，点M以每秒3个单位长度的速度从点A向点Q运动，同时，点N以每秒1个单位长度的速度从点C向点Q运动，当点M、N中有一点到达Q点时，两点同时停止运动，设运动时间为t秒．

    ①连接AN，当△AMN的面积最大时，求t的值；

    ②线段PQ能否垂直平分线段MN？如果能，请求出此时直线PQ的函数关系式；如果不能请说明你的理由．

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如下图，当宽为3 cm的刻度尺的一边与圆相切时，另一边与圆的两个交点处的读数如图所示（单位：cm），那么该圆的半径为

    A．                     B．                        C．5                            D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某车库出口处设置有“两段式栏杆” ，点A是栏杆转动的支点，点E是栏杆两段的连接点，当车辆经过时，栏杆AEF升起后的位置如图1所示（图2为其几何图形）。其中AB⊥BC，DC⊥BC，EF∥BC，∠EAB＝150°，AB＝AE＝1.2 m，BC＝2.4m。

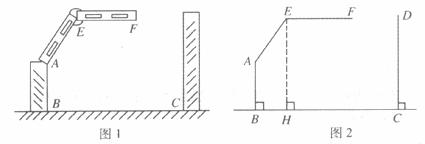
    （1）求图2中点E到地面的高度（即EH的长。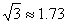，结果精确到0.01 m，栏杆宽度忽略不计）；

    （2）若一辆厢式货车的宽度和高度均为2 m，这辆车能否驶入该车库？请说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在矩形ABCD中，由8个面积均为1的小正方形组成的L型模板如图放置，则矩形ABCD的周长为（      ）

      A.4              B.8    C.6              D.12

     

    查看答案和解析>>

    同步练习册答案