
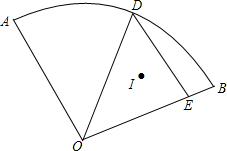
 如图所示扇形AOB中,∠AOB=90°,OA=OB=6,D为弧上一动点,过D作DE∥OA交OB于点E.I为△ODE的内心,当点D运动时,I也随着运动.则经过O、I、B三点的弧所在圆的半径为3$\sqrt{2}$.
如图所示扇形AOB中,∠AOB=90°,OA=OB=6,D为弧上一动点,过D作DE∥OA交OB于点E.I为△ODE的内心,当点D运动时,I也随着运动.则经过O、I、B三点的弧所在圆的半径为3$\sqrt{2}$. 分析 连接OI、DI、BD,以OD为弦作圆C,在圆C上取一点F.I是△ODE的内心,则三角形I是三角形条角平分线的交点,故此可求得∠OID=135°,∠DOI=∠BOI,于是可证明△△DOI≌△BOI,得到∠OIB=∠OID=135°,故此点I在以OB为弦且所对的圆周角为135°的一段劣弧上,由圆内接四边形的性质可知∠F=45°,由圆周角定理可求得∠OCD=90°,最后利用特殊锐角三角函数可求得OC=3$\sqrt{2}$.
解答 解:如图所示:连接OI、DI、BD,以OD为弦作圆C,在圆C上取一点F.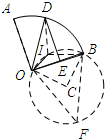
∵I是△ODE的内心,
∴∠IDO=$\frac{1}{2}$∠EDO,∠DOI=$\frac{1}{2}$∠DOB.
∴∠IDO+∠DOI=$\frac{1}{2}$(∠EDO+∠DOB)=$\frac{1}{2}×90°$=45°.
∴∠OID=45°.
∵I是△ODE的内心,
∴∠DOI=∠BOI.
在△DOI和△BOI中,
$\left\{\begin{array}{l}{OD=OB}\\{∠DOI=∠BOI}\\{OI=OI}\end{array}\right.$,
∴△△DOI≌△BOI.
∴∠OIB=∠OID=135°.
∴点I在以OB为弦且所对的圆周角为135°的一段劣弧上.
∵四边形OFDI是圆内接四边形,
∴∠F+∠OID=180°.
∴∠F=45°.
∴∠OCD=90°.
∵CO=CB,
∴∠COD=45°.
∴OC=$\frac{\sqrt{2}}{2}$×OB=$\frac{\sqrt{2}}{2}×6$=3$\sqrt{2}$.
故答案为:3$\sqrt{2}$.
点评 本题主要考查的是三角形的内心、全等三角形的性质和判定、特殊锐角三角函数,圆内接四边形的性质,证得点I在以OB为弦且所对的圆周角为135°的一段劣弧上是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
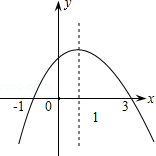 如图是二次函数y=ax2+bx+c的图象,下列结论:
如图是二次函数y=ax2+bx+c的图象,下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
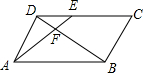 如图,在平行四边形ABCD中,E为CD上一点,连结AE,BD,且AE,BD交于点F,S△DEF:S△ABF=4:25,求DE:DC的值为( )
如图,在平行四边形ABCD中,E为CD上一点,连结AE,BD,且AE,BD交于点F,S△DEF:S△ABF=4:25,求DE:DC的值为( )| A. | 4:25 | B. | 2:5 | C. | 2:7 | D. | 4:29 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com