练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．已知a-b=2，b-c=-1，求a2+b2+c2-ab-bc-ca的值．

    分析 首先由a-b=3，b-c=-1，求得a-c=2，再将a2+b2+c2-ab-bc-ca变形为$\frac{1}{2}$（2a2+2b2+2c2-2ab-2bc-2ca），即得$\frac{1}{2}$[（a-b）2+（a-c）2+（b-c）2]，代入求值即可．

    解答 解：原式=$\frac{1}{2}$（2a2+2b2+2c2-2ab-2bc-2ac）
    =$\frac{1}{2}$[（a-b）2+（a-c）2+（b-c）2]
    ∵a-b=2，b-c=-1，
    ∴a-c=1，
    ∴原式=$\frac{1}{2}$×[22+12+（-1）2]=3．

    点评 此题考查了利用完全平方公式因式分解的应用．注意整体思想的渗透，将原式变形为完全平方式的和是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    11．把二次函数y=x2-6x-3化为顶点式为y=（x-3）2-12．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．求证：函数y=mx2-（3m-1）x+2m-2的图象与x轴必有交点．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．计算：
    （1）$\frac{x}{x-1}$-1    
    （2）$\frac{2x}{10x-6}$÷$\frac{3}{25{x}^{2}-9}$•$\frac{x}{3+5x}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．在数轴上有100个点，它们分别是P1，P2，P3，…P99，P100，从左到右依次成等距离排列，即有P1P2=P2P3=P3P4=…P99P100，则当点P4和P9在数轴上所表示的数分别为-7和33时，点P100所表示的数是761．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

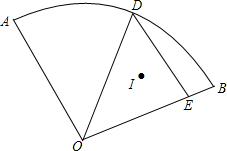    3．如图所示扇形AOB中，∠AOB=90°，OA=OB=6，D为弧上一动点，过D作DE∥OA交OB于点E．I为△ODE的内心，当点D运动时，I也随着运动．则经过O、I、B三点的弧所在圆的半径为3$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．如图，有一块形如等腰直角三角形的木板，直角边长为a，要用它截出一块矩形木板DEFG，则矩形木板DEFG的面积不可能是（　　）
    A．$\frac{{a}^{2}}{6}$B．$\frac{{a}^{2}}{5}$C．$\frac{{a}^{2}}{4}$D．$\frac{{a}^{2}}{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．化简求值$\frac{{m}^{2}-2m+1}{{m}^{2}-1}$÷（m-1-$\frac{m-1}{m+1}$），其中m=-3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．已知a，b，c在数轴上对应的点的位置如图所示：化简：|b+c|+|a+c|-|b-a|-|a+b+c|．

    查看答案和解析>>

    同步练习册答案