
 如图,有一块形如等腰直角三角形的木板,直角边长为a,要用它截出一块矩形木板DEFG,则矩形木板DEFG的面积不可能是( )
如图,有一块形如等腰直角三角形的木板,直角边长为a,要用它截出一块矩形木板DEFG,则矩形木板DEFG的面积不可能是( )| A. | $\frac{{a}^{2}}{6}$ | B. | $\frac{{a}^{2}}{5}$ | C. | $\frac{{a}^{2}}{4}$ | D. | $\frac{{a}^{2}}{3}$ |
分析 设DG为x,过点A作AH⊥BC,交DG于点M,垂足为H,根据已知条件可知△ADG∽△ABC,从而可以用含x的代数式表示AM,利用矩形面积公式可得y与x之间的函数关系式;根据公式法,结合已求得的二次函数解析式求得最大值,进一步分析得出答案即可.
解答 解:(1)如图所示,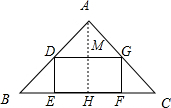
过点A作AH⊥BC,垂足为H,交DG于点M,
在Rt△ABC中,AB=AC=a,
由勾股定理得:BC=$\sqrt{2}$a.
∵AH⊥BC,
∴△ABH为等腰直角三角形.
∴AH=BH=$\frac{\sqrt{2}}{2}$a.
∵四边形DEFG是矩形,
∴DG∥BC,
∴△ADG∽△ABC.
∴$\frac{AM}{AH}$=$\frac{DG}{BC}$,设DG为x,
即$\frac{AM}{\frac{\sqrt{2}}{2}a}$=$\frac{x}{\sqrt{2}a}$,
∴AM=$\frac{1}{2}$x
∴DE=$\frac{\sqrt{2}}{2}$a-$\frac{1}{2}$x.
∴矩形木板DEFG的面积y=x($\frac{\sqrt{2}}{2}$a-$\frac{1}{2}$x)=-$\frac{1}{2}$x2+$\frac{\sqrt{2}}{2}$ax;
∵a=-$\frac{1}{2}$<0,函数有最大值,
∴y=-$\frac{1}{2}$x2+$\frac{\sqrt{2}}{2}$ax=-$\frac{1}{2}$(x-$\frac{\sqrt{2}}{2}$a)2+$\frac{{a}^{2}}{4}$,
当x=$\frac{\sqrt{2}}{2}$a时,
y最大值=$\frac{{a}^{2}}{4}$,
即矩形木板DEFG的面积最大是$\frac{{a}^{2}}{4}$.
只有D选项不合题意.
故选:D.
点评 此题考查相似三角形的判定与性质,矩形的性质,二次函数的最值,利用相似的性质和矩形的面积求得二次函数解析式是解决问题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
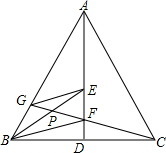 如图,AD是等腰△ABC底边上的高,E、F为AD上两点,且∠ABE=∠EBF=∠FBC,连接CF并延长交AB于点G,求证:
如图,AD是等腰△ABC底边上的高,E、F为AD上两点,且∠ABE=∠EBF=∠FBC,连接CF并延长交AB于点G,求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com