【题目】如图，在平面直角坐标系xOy中，A点的坐标为（1，0）．以OA为边在x轴上方画一个正方形OABC．以原点O为圆心，正方形的对角线OB长为半径画弧，与x轴正半轴交于点D．

（1）点D的坐标是 ；

（2）点P（x，y），其中x，y满足2x-y=-4．

①若点P在第三象限，且△OPD的面积为3，求点P的坐标；

②若点P在第二象限，判断点E（+1，0）是否在线段OD上，并说明理由．

参考答案：

【答案】（1）（，0）；（2）①P（-5，-6）；②点E在线段OD上，见解析.

【解析】

（1）先求出正方形的边长，再用勾股定理求出OB，即可得出结论；

（2）①先表示出PQ，再利用△ODP的没解决建立方程求解，即可得出结论；

②根据点P在第二象限，求出x的范围，进而判断出点E在x轴正半轴上，即可得出结论．

（1）∵四边形OABC是正方形，且A（1，0），

∴OA=AB=1，

根据勾股定理得，OB=，

∴OD=，

∴D（，0），

故答案为：（，0）；

（2）①如图，过点P作PQ⊥x轴于点Q，

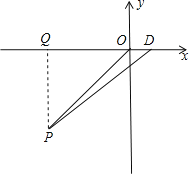
∵点P在第三象限，

∴y=2x+4＜0，

∴PQ=-（2x+4），

∵D（，0），

∴OD=，

∴S△ODP=ODPQ=3，

即：-××(2x+4)＝3，

∴x=-5，

∴P（-5，-6）；

②点E在线段OD上，

理由：∵2x-y=-4，

∴y=2x+4，

∵点P在第二象限，

∴，

∴-2＜x＜0，

∴0＜x+1＜1，

∴点E在x轴正半轴上，

∵点D在x轴正半轴，OD=，

∴0＜OE＜OD，

∴点E在线段OD上．

关闭