
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:选择题
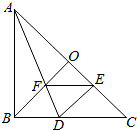 如图,在Rt△ABC中,AB=CB,BO⊥AC,把△ABC折叠,使AB落在AC上,点B与AC上的点E重合,展开后,折痕AD交BO于点F,连接DE、EF,下列结论:①AB=2BD;②图中有4对全等三角形;③若将△DEF沿EF折叠,则点O不一定落在AC上;④BD=BF,上述结论中正确的是( )
如图,在Rt△ABC中,AB=CB,BO⊥AC,把△ABC折叠,使AB落在AC上,点B与AC上的点E重合,展开后,折痕AD交BO于点F,连接DE、EF,下列结论:①AB=2BD;②图中有4对全等三角形;③若将△DEF沿EF折叠,则点O不一定落在AC上;④BD=BF,上述结论中正确的是( )| A. | ①②③④ | B. | ②④ | C. | ①③④ | D. | ①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
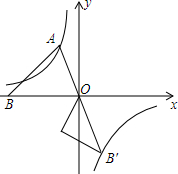 如图,已知第二象限的点A在反比例函数y=-$\frac{\sqrt{3}}{x}$上,过点A作AB⊥AO交x轴于点B,∠AOB=60°.将△AOB绕点O逆时针旋转120°,点B的对应点B′恰好落在反比例函数y=$\frac{k}{x}$上,则k的值为( )
如图,已知第二象限的点A在反比例函数y=-$\frac{\sqrt{3}}{x}$上,过点A作AB⊥AO交x轴于点B,∠AOB=60°.将△AOB绕点O逆时针旋转120°,点B的对应点B′恰好落在反比例函数y=$\frac{k}{x}$上,则k的值为( )| A. | -2$\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | -4$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第一、三象限 | B. | 第二、四象限 | C. | 第三、四象限 | D. | 第一、二象限 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 学校要围一个矩形花圃,其一边利用足够长的墙,另三边用篱笆围成,由于园艺需要,还要用一段篱笆将花圃分隔为两个小矩形部分(如图所示),总共36米的篱笆恰好用完(不考虑损耗).设矩形垂直于墙面的一边AB的长为x米(要求AB<AD),矩形花圃ABCD的面积为S平方米.
学校要围一个矩形花圃,其一边利用足够长的墙,另三边用篱笆围成,由于园艺需要,还要用一段篱笆将花圃分隔为两个小矩形部分(如图所示),总共36米的篱笆恰好用完(不考虑损耗).设矩形垂直于墙面的一边AB的长为x米(要求AB<AD),矩形花圃ABCD的面积为S平方米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com