
【题目】如图,数轴上每相邻两点的相距一个单位长度,点A、B、C、D是这些点中的四个,且对应的位置如图所示,它们对应的数分别是a,b,c,d.
(1)当ab=﹣1,则d= .
(2)若|d﹣2a|=7,求点C对应的数.
(3)若abcd<0,a+b>0,化简|a﹣b|﹣|b+c﹣5|﹣|c﹣5|﹣|d﹣a|+|8﹣d|.
![]()
【答案】(1)8;(2)C对应的点就为7或21;(3)﹣8.
【解析】
(1)根据每相邻两点的相距一个单位长度,且积为﹣1,可得a,b,进而得d;
(2)由绝对值的含义化简绝对值,得到d﹣2a=±7,并结合图形可分类讨论求解;
(3)由abcd<0,a<b<c<d,得到a,b,c为负数,d为正数;或者a为负数,b,c,d为正数.又因为a+b>0,可得a为负数,b,c,d为正数;再结合图形,分析可化简绝对值,再合并同类项即可.
(1)因为每相邻两点的相距一个单位长度,
所以a,b为整数
又ab=﹣1,
所以a=﹣1,b=1,
所以d=8
故答案为:8;
(2)因为|d﹣2a|=7所以d﹣2a=±7;
由图知:d﹣a=9;
ⅰ.当d﹣2a=7 时,9﹣a=7,则a=2,所以 C 对应的点就为 7;
ⅱ.当d﹣2a=﹣7 时,9﹣a=﹣7,则a=16,所以 C 对应的点就为 21.
(3)因为abcd<0,a<b<c<d,
所以a,b,c为负数,d为正数;或者a为负数,b,c,d为正数.
又因为a+b>0,所以a为负数,b,c,d为正数;
由题与图可得:﹣1<a<0,1<b<2,4<c<5,8<d<9;
因为a﹣b<0,b+c>0,c﹣5<0,d﹣a>0,8﹣d<0
所以a﹣b﹣b+c﹣5﹣c﹣5﹣d﹣a+8﹣d
=b﹣a﹣(b+c﹣5)+(c﹣5)﹣(d﹣a)﹣(8﹣d )
=b﹣a﹣b﹣c+5+c﹣5﹣d+a﹣8+d
=﹣8.


科目:初中数学 来源: 题型:
【题目】解密数学魔术:魔术师请观众心想一个数,然后将这个数按以下步骤操作:![]()
魔术师能立刻说出观众想的那个数.
(1)如果小玲想的数是-1,那么她告诉魔术师的结果应该是 ;
(2)如果小明想了一个数计算后,告诉魔术师结果为93,那么魔术师立刻说出小明想的那个数是 ;
(3)观众又进行了几次尝试,魔术师都能立刻说出他们想的那个数.若设观众心想的数为a,请通过计算解密这个魔术的奥妙.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的平分线,
的平分线,![]() 是
是![]() 的平分线.
的平分线.
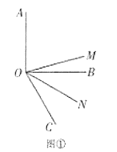
(1)如图①,当![]() 是直角,
是直角,![]() 时,
时,![]() __________,
__________,![]() __________,
__________,![]() __________;
__________;
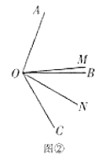
(2)如图②,当![]() ,
,![]() 时,猜想:
时,猜想:![]() 的度数与
的度数与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
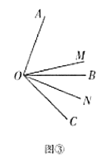
(3)如图③,当![]() ,
,![]() (
(![]() 为锐角)时,猜想:
为锐角)时,猜想:![]() 的度数与
的度数与![]() ,
,![]() 有怎样的数量关系?请写出结论,并说明理由.
有怎样的数量关系?请写出结论,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
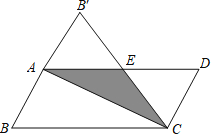
【题目】如图,在平行四边形纸片ABCD中,AB=3cm,将纸片沿对角线AC对折,BC边的对应边B′C与AD边交于点E,此时△CDE恰为等边三角形中,求:
(1)AD的长度.
(2)重叠部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
(1)求证:BD=CD;
(2)请判断B,E,C三点是否在以D为圆心,以DB为半径的圆上?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
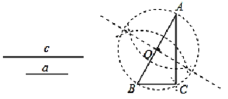
【题目】数学课上,老师让学生尺规作图画Rt△ABC,使其斜边AB=c,一条直角边BC=a.李明的作法如图所示,作线段AB使AB=C,以AB为直径作⊙O,以B为圆心,a为半径作弧交⊙O于点C,连接AC,△ABC即为所求作的三角形,你认为这种作法中判断∠ACB是直角的依据是( )
A. 90°的圆周角所对的弦是直径 B. 直径所对的圆周角是直角
C. 勾股定理的逆定理 D. 勾股定理
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图将矩形ABCD的四个内角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12,EF=16,则边AB的长是( )

A. 8+6![]() B. 12
B. 12![]() C. 19.2D. 20
C. 19.2D. 20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中央电视台的“中国诗词大赛”节目文化品位高,内容丰富,某校初二年级模拟开展“中国诗词大赛”比赛,对全年级同学成绩进行统计后分为“优秀”、“良好”、“一般”、“较差”四个等级,并根据成绩绘制成如下两幅不完整的统计图,请结合统计图中的信息,回答下列问题:

(1)扇形统计图中“优秀”所对应的扇形的圆心角为 度,并将条形统计图补充完整.
(2)此次比赛有四名同学活动满分,分别是甲、乙、丙、丁,现从这四名同学中挑选两名同学参加学校举行的“中国诗词大赛”比赛,请用列表法或画树状图法,求出选中的两名同学恰好是甲、丁的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种股票第一天的最高价比开盘价高0.3元,最低价比开盘价低0.2元;第二天的最高价开盘价高0.2元,最低价比开盘价低0.1元;第三天的最高价等于开盘价,最低价比开盘价低0.13元.计算每天最高价与最低价的差,以及这些差的平均值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com