
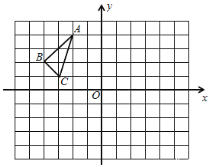
����Ŀ����ABC��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ������ÿ��С�����εı߳�Ϊ1����λ���ȣ�
��1����Ҫ����ͼ��
�ٻ�����ABC����ԭ��O�����ĶԳ�ͼ�Ρ�A1B1C1��
�ڻ�������ABC�Ƶ�O˳ʱ����ת90���õ���A2B2C2��
��2�����գ�1���Т���ͼ���ش��������⣺��A2B2C2�ж���A2����Ϊ�� ����B2������Ϊ�� ������P��a��b��Ϊ��ABC����һ�㣬���P��Ӧ�ĵ�Q������Ϊ�� ����
���𰸡���1������������2����4��2������2��4������b����a����
��������
(1)�ҳ���A��B��C����ԭ��O�ĶԳƵ��λ��,Ȼ��˳�����Ӽ���;��������ṹ�Լ�ƽ��ֱ������ϵ���ص�,�ҳ���A��B�Ƶ�O˳ʱ����ת90���Ķ�Ӧ���λ��,Ȼ��˳�����Ӽ���
��2����ͼ���ٸ���ƽ��ֱ������ϵ���ص�д��������꼴��
�⣺��1������ͼ��ʾ����A1B1C1��Ϊ����
����ͼ��ʾ����A2B2C2��Ϊ����

��2����ͼ֪����A2����Ϊ��4��2����B2������Ϊ��2��4����
��P��a��b��Ϊ��ABC����һ�㣬���P��Ӧ�ĵ�Q������Ϊ��b����a����
�ʴ�Ϊ����4��2������2��4������b����a����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����OΪԭ���ֱ������ϵ�У�A�������Ϊ��0��1����ֱ��x=1��x���ڵ�B����Ϊ�߶�AB��һ���㣬��ֱ��PC��PO����ֱ��x=1�ڵ�C����P����ֱ��MNƽ����x�ᣬ��y���ڵ�M����ֱ��x=1�ڵ�N����AP=x����PBC�����ΪS��
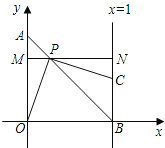
��1������C�ڵ�һ����ʱ����֤����OPM�ա�PCN��
��2������P���߶�AB���ƶ�ʱ����CҲ��֮��ֱ��x=1���ƶ������S��x֮��ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ��
��3������P���߶�AB���ƶ�ʱ����PBC�Ƿ���ܳ�Ϊ���������Σ�������ܣ�ֱ��д��������ʹ��PBC��Ϊ���������ε�x��ֵ����������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
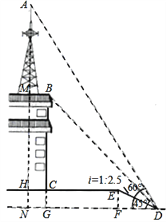
����Ŀ����ͼ��ijУ���깬��ѧ��������С���ͬѧΪ����һ������AM�ĸ߶���ͼ���������¶���i=1:2��5��б��DE��D�������¥�����ƶ�ͨѶ��վ�����Ķ���A��¥��B�����Ƿֱ���60����45����б�¸�EF=2�ף�CE=13�ף�CH=2�ס���Ҹ�����ѧ֪ʶ�ܿ�������������AM���װ���ͬѧ�ǣ�������Ҳ�ܼ��������AM�ĸ߶ȣ�����д�������̡�������![]() ��1��41��
��1��41�� ![]() ��1��73��ѡ�ã��������������
��1��73��ѡ�ã��������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ�����ͼ���뷴��������![]() ��ͼ����A����2,6���͵�B��4,n��
��ͼ����A����2,6���͵�B��4,n��
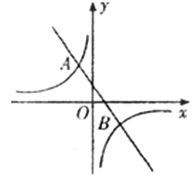
��1�����������Ľ���ʽ��B������
��2������ͼ��ش�,��ʲô��Χʱ,һ�κ�����ֵ���ڷ�����������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������������ͼ����P��2����3����
��1����ú����Ľ���ʽ��
��2��������P��x�Ḻ����ƽ��3����λ������y�᷽��ƽ��n��n��0������λ�õ���P�䣬ʹ��P��ǡ���ڸú�����ͼ���ϣ���n��ֵ�͵�P��y��ƽ�Ƶķ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У��ı���AOBC�Ǿ��Σ���O��0��0������A��5��0������B��0��3�����Ե�AΪ���ģ�˳ʱ����ת����AOBC���õ�����ADEF����O��B��C�Ķ�Ӧ��ֱ�ΪD��E��F���ҵ�Dǡ������BC���ϣ�
��1����ԭͼ�ϻ�����ת��ľ��Σ�
��2�����ʱ��D�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
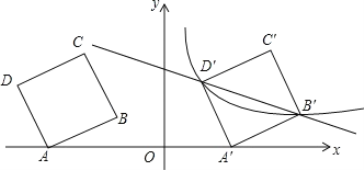
����Ŀ����ͼ,��ƽ��ֱ������ϵ��,�ı���ABCDΪ������,��֪��A(-6,0),D(-7,3)����B��C�ڵڶ������ڣ�
(1)��B������ ��
(2)��������ABCD��ÿ��1����λ���ٶ���x������ƽ��t��,������ijһʱ��t,ʹ�ڵ�һ�����ڵ�B��D����Ķ�Ӧ��B����D����������ij������������ͼ���ϣ��������ʱt��ֵ�Լ���������������Ľ���ʽ��
(3)��(2)�������,���Ƿ����x���ϵĵ�P�ͷ���������ͼ���ϵĵ�Q,ʹ����P��Q��B����D���ĸ���Ϊ������ı�����ƽ���ı���?�����ڣ��������������ĵ�P��Q�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���C=90������B=30������AΪԲ�ģ����ⳤΪ�뾶�����ֱ�AB��AC�ڵ�M��N���ٷֱ���M��NΪԲ�ģ�����MN�ij�Ϊ�뾶�������������ڵ�P������AP���ӳ���BC�ڵ�D��������˵������ȷ�ĸ�����
��AD����BAC��ƽ���ߣ��ڡ�ADC=60��������D��AB���д����ϣ���S��DAC��S��ABC=1��3��

A��1 B��2 C��3 D��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ ABCD �У�AB=8��BC=6�������� ABCD �Ƶ� A ��ʱ����ת�õ����� AEFG��AE��FG �ֱ�����CD �ڵ� PH������ AH���� P �� CH ���е㣬����APH ���ܳ�Ϊ�� ��
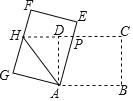
A. 15 B. 18 C. 20 D. 24
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com