
����Ŀ��ij�쳵�ļƷѹ������1��С�����γ����쳵��������2������ϸ�۲�����������������⣺
��1����գ�a���� ����b���� ����
��2���з�������1�е�x��
��3��С���İְ�23��10��쳵�ӻ����ؼң��쳵��ʻ��ƽ���ٶ���100����/Сʱ�����Һ�С���ְ�֧������603Ԫ�����ʻ�����С���ҵ�·���Ƕ��ٹ�����÷��̽�������⣩
��1��ij�쳵�ļƷѹ���
��̷ѣ�Ԫ/��� | ʱ���ѣ�Ԫ/���ӣ� | Զ;�ѣ�Ԫ/��� | |||
5��00��23��00 | a | 9��00��18��00 | x | 12���P���� | 0 |
23��00������5��00 | 3.2 | 18��00������9��00 | 0.5 | ����12����IJ��� | 1.6 |
��˵�����ܷ��ã���̷�+ʱ����+Զ;�ѣ�
��2��С�����γ����쳵��Ϣ
�ϳ�ʱ�� | ��̣���� | ʱ�������ӣ� | Զ;�ѣ�Ԫ�� | �ܷ��ã�Ԫ�� |
7��30 | 5 | 5 | 0 | 13.5 |
10��05 | 20 | 18 | 66.7 |
���𰸡���1��2.2��12.8����2��x��0.55����3��������С���ҵ�·����122���
��������
��1�����ݱ��������з��̣������a��ֵ��b��ֵ�������мƷѷ�ʽ��ʽ���㼴�ɣ�
��2��������̷�+ʱ����+Զ;�ѣ��ܷ��ã��з�����⼴�ɣ�
��3���������С���ҵ�·����y�������ҹ��˳��ļƷѷ�ʽ���з�����⼴�ɣ�
�⣺��1��������ã�5a+5��0.5��13.5
��ã�a��2.2
b����20��12����1.6��12.8
�ʴ�Ϊ��2.2��12.8��
��2��������ã�20��2.2+12.8+18x��66.7
18x��9.9
x��0.55
��3���������С���ҵ�·����y�����
3.2y+0.5��![]() ��60+��y��12����1.6��603
��60+��y��12����1.6��603
���y��122
�𣺻�����С���ҵ�·����122���


 ��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�
��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬BD�ǽ�ƽ���ߣ���O��AB�ϣ��Ե�OΪԲ�ģ�OBΪ�뾶��Բ������D����BC�ڵ�E��
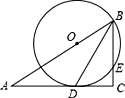
��1����֤��AC�ǡ�O�����ߣ�
��2����OB=5��CD=4����BE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0����ͼ����ͼ�����������ĸ����ۣ���4ac��b2��0����4a+c��2b����3b+2c��0����m��am+b��+b��a��m�٩�1����������ȷ���۵���_________��ֻ����ţ�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ1����֪A��B�����߳�����ȵ�������ֽƬ���ŷ��ã���m7��n3������A��B����������ֽƬ�����֮�ͣ�
��2����ͼ1����m��n��ʾA��B����������ֽƬ�����֮��Ϊ ������ֱ��д���𰸣�
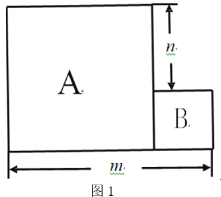
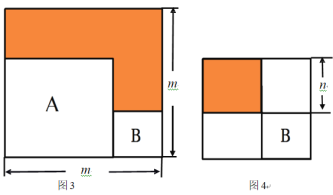
��3����ͼ2����A��B����������ֽƬ�����֮��Ϊ5����ͼ2����Ӱ���ֵ����Ϊ2������m��n��ֵ��

��4���ֽ�������ֽƬA��B���ŷ��ú����µ������ε�ͼ3����������ֽƬB����������ֽƬA���ڲ���ͼ4����ͼ3��ͼ4����Ӱ���ֵ�����ֱ�Ϊ12��1����A��B����������ֽƬ�����֮��Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����������A�Ͽ��������������Ĵ���BC�������B��C����ĸ��Ƿֱ�Ϊ45�㣬36�㣮��֪����BC�������ͬһˮƽ���ϣ��䳤��Ϊ100m������������������ĸ߶ȣ��������С�����һλ�����ο����ݣ�tan36����0.73��
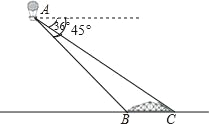
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ����У���ƻ������Ϊ2000m2����������̻������żס����������̶���ɣ���֪��ÿ������̻���������Ҷ�ÿ������̻��������2���������ڶ���������Ϊ600m2������̻�ʱ���ӱ��Ҷ�����6�죮
��1���ס����������̶�ÿ��������̻�������ֱ��Ƕ��٣�
��2����ѧУÿ���踶���ӵ��̻�����Ϊ0.5��Ԫ���Ҷ�Ϊ0.3��Ԫ��Ҫʹ��ε��̻��ܷ��ò�����10��Ԫ������Ӧ���żӹ��������죿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ϵ�A��ʾ����a����B��ʾ��b��a��b����|a��40|+��b+8��2��0����O������ԭ�㣮
![]()
��1����A��ʾ����Ϊ ����B��ʾ����Ϊ ���߶�AB�ij�Ϊ ��
��2������A���C֮��ľ����ʾΪAC����B���C֮��ľ����ʾΪBC��������������һ��C��ʹAC��2BC�����C�������ϱ�ʾ����Ϊ ��
��3�����ж���P��Q����B���������P��ÿ��1����λ���ȵ��ٶ����յ�A�ƶ�������P�ƶ���O��ʱ����Q�Ŵ�B�����������ÿ��3����λ���ȵ��ٶ������ƶ����ҵ���P����A��ʱ����Q��ֹͣ�ƶ������P�ƶ���ʱ��Ϊt�룬�ʣ���tΪ����ʱ��P��Q�������4����λ���ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���D�DZ�BC���е㣬��E����ABC�ڣ�AEƽ����BAC��CE��AE����F�ڱ�AB�ϣ�EF��BC��

��1����֤���ı���BDEF��ƽ���ı��Σ�
��2���߶�BF��AB��AC������֮����������Ĺ�ϵ��֤�������õ��Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ABCD�У�AB=8����P�ڱ�CD�ϣ�tan��PBC=![]() ����Q��������BP�ϵ�һ�����㣬����Q��AB��ƽ���߽�����AD�ڵ�M����R������AD�ϣ�ʹRQʼ����ֱ��BP��ֱ��
����Q��������BP�ϵ�һ�����㣬����Q��AB��ƽ���߽�����AD�ڵ�M����R������AD�ϣ�ʹRQʼ����ֱ��BP��ֱ��
��1����ͼ1������R���D�غ�ʱ����PQ�ij���
��2����ͼ2����̽���� ![]() �ı�ֵ�Ƿ����Q���˶��������仯�����б仯����˵��������ɣ���û�б仯����������ı�ֵ��
�ı�ֵ�Ƿ����Q���˶��������仯�����б仯����˵��������ɣ���û�б仯����������ı�ֵ��
��3����ͼ3������Q���߶�BP�ϣ���PQ=x��RM=y����y����x�ĺ�����ϵʽ����д�����Ķ�����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com