
如图,直线⊥线段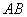 于点
于点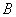 ,点
,点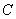 在
在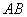 上,且
上,且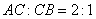 ,点
,点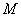 是直线上的动点,作点
是直线上的动点,作点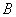 关于直线
关于直线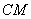 的对称点
的对称点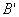 ,直线
,直线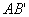 与直线
与直线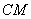 相交于点
相交于点 ,连接
,连接
(1)如图1,若点 与点
与点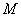 重合,则∠
重合,则∠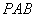 = °,线段
= °,线段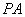 与
与 的比值为 ;
的比值为 ;
(2)如图2,若点 与点
与点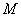 不重合,设过
不重合,设过 、
、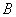 、
、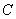 三点的圆与直线
三点的圆与直线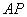 相交于
相交于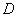 ,
,
连接 。
。
求证:① =
=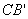 ;②
;②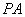 =2
=2 ;
;
(3)如图3,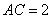 ,
, ,则满足条件
,则满足条件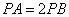 的点都在一个确定的圆上,在
的点都在一个确定的圆上,在
以下两小题中选做一题:
①如果你能发现这个确定圆的圆心和半径,那么不必写出发现过程,只要证明这个
圆上的任意一点Q,都满足QA=2QB
②如果你不能发现这个确定圆的圆心和半径,那么请取几个特殊位置的 点,如点
点,如点 在直线
在直线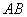 上、点
上、点 与点
与点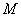 重合等进行探究,求这个圆的半径
重合等进行探究,求这个圆的半径

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1OD的面积是( )

|
| A. |
| B. |
| C. |
| D. |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系中,抛物线y=x2+5x+4的顶点为M,与x轴交于A,B两点,与y轴交于C点.
(1)求点A,B,C的坐标;
(2)求抛物线y=x2+5x+4关于坐标原点O对称的抛物线的函数表达式;
(3)设(2)中所求抛物线的顶点为M′,与x轴交于A′,B′两点,与y轴交于C′点,在以A,B,C,M,A′,B′,C′,M′这八个点中的四个点为顶点的平行四边形中,求其中一个不是菱形的平行四边形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知Rt△ABC中,∠ABC=90°,AC=6,BC=4,将△ABC绕直角顶点C顺时
针旋转90°得到△DEC,若点F是DE的中点,连接AF,则AF= 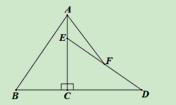
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,将□ABCD沿过点A的直线折叠,使点D落到AB边上的 点
 处,折痕交CD边于点E,连接BE
处,折痕交CD边于点E,连接BE
(1)求证:四边形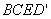 是平行四边形
是平行四边形
(2)若BE平分∠ABC,求证:
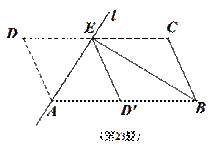
查看答案和解析>>
科目:初中数学 来源: 题型:
我们解一元二次方程3x2﹣6x=0时,可以运用因式分解法,将此方程化为3x(x﹣2)=0,从而得到两个一元一次方程:3x=0或x﹣2=0,进而得到原方程的解为x1=0,x2=2.这种解法体现的数学思想是( )
|
| A. | 转化思想 | B. | 函数思想 | C. | 数形结合思想 | D. | 公理化思想 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图是一组有规律的图案,它们是由边长相同的正方形和正三角形镶嵌而成,第(1)个图案有4个三角形,第(2)个图案有7个三角形,第(3)个图案有10个三角形,…依此规律,第n个图案有 个三角形(用含n的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
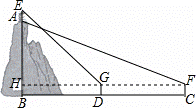
学习“利用三角函数测高”后,某综合实践活动小组实地测量了凤凰山与中心广场的相对高度AB,其测量步骤如下:
(1)在中心广场测点C处安置测倾器,测得此时山顶A的仰角∠AFH=30°;
(2)在测点C与山脚B之间的D处安置测倾器(C、D与B在同一直线上,且C、D之间的距离可以直接测得),测得此时山顶上红军亭顶部E的仰角∠EGH=45°;
(3)测得测倾器的高度CF=DG=1.5米,并测得CD之间的距离为288米;
已知红军亭高度为12米,请根据测量数据求出凤凰山与中心广场的相对高度AB.( 取1.732,结果保留整数)
取1.732,结果保留整数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com