
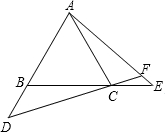
如图:已知在等边三角形ABC中,点D、E分别是AB、BC延长线上的点,且BD=CE,直线CD与AE相交于点F.
(1)求证:DC=AE;
(2)求证:AD2=DC•DF.
【考点】相似三角形的判定与性质;全等三角形的判定与性质;等边三角形的性质.
【分析】(1)利用“SAS”证明△DBC≌△ECA即可;
(2)由△DBC≌△ECA可知∠E=∠D,根据外角定理可知∠AFC=∠E+∠FCE=∠D+∠BCD=∠ABC=60°,可证△DCA∽△DAF,利用相似比得出结论.
【解答】证明:(1)∵△ABC是等边三角形,
∴∠ABC=∠ACB=∠BAC=60°,BC=CA
∴∠DBC=∠ECA=180°﹣60°=120°
在△DBC与△ECA中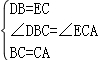
∴△DBC≌△ECA(SAS)
∴DC=AE;
(2)∵△DBC≌△ECA,
∴∠DCB=∠EAC
又∠ACB=∠BAC
∴∠DCA=∠DAF
又∠D=∠D
∴△DCA∽△DAF
∴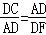
∴AD2=DC•DF.
【点评】本题考查了全等三角形、相似三角形的判定与性质.关键是根据等边三角形的性质找角相等的条件.


科目:初中数学 来源: 题型:
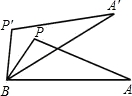
如图,如果△APB绕点B按逆时针方向旋转30°后得到△A′P′B,且BP=2,那么PP′的长为__________.(不取近似值.以下数据供解题使用:sin15°=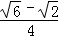 ,cos15°=
,cos15°=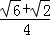 )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系中,点B的坐标为(3,1),则点B关于原点的对称点的坐标为
A. (3,-1) B. (-3,1) C. (-1,-3) D. (-3,-1)
查看答案和解析>>
科目:初中数学 来源: 题型:
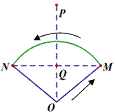
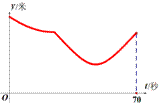
小阳在如图①所示的扇形舞台上沿O-M-N匀速行走,他从点O出发,沿箭头所示的方向经过点M再走到点N,共用时70秒.有一台摄像机选择了一个固定的位置记录了小阳的走路过程,设小阳走路的时间为t(单位:秒),他与摄像机的距离为y(单位:米),表示y与t的函数关系的图象大致如图②,则这个固定位置可能是图①中的
A. 点Q B. 点P C. 点M D. 点N
查看答案和解析>>
科目:初中数学 来源: 题型:
我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段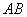 的最小覆盖圆就是以线段
的最小覆盖圆就是以线段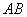 为直径的圆.
为直径的圆.
(1)请分别作出图①中两个三角形的最小覆盖圆(要求用尺规作图,保留作图痕迹,不写作法);
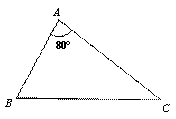
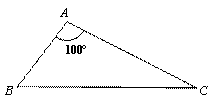
图①
 (2)三角形的最小覆盖圆有何规律?请直接写出你所得到的结论(不要求证明);
(2)三角形的最小覆盖圆有何规律?请直接写出你所得到的结论(不要求证明);
(3)某城市有四个小区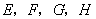 (其位置如图②所示),现拟建一个手机信号基站,为了使这四个小区居民的手机都能有信号,且使基站所需发射功率最小(距离越小,所需功率越小),此基站应建在何处?请写出你的结论并说明研究思路.
(其位置如图②所示),现拟建一个手机信号基站,为了使这四个小区居民的手机都能有信号,且使基站所需发射功率最小(距离越小,所需功率越小),此基站应建在何处?请写出你的结论并说明研究思路.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com