Question

已知：在△ABC中，∠BAC=90°，AB=AC，AE是过点A的一条直线，且BD⊥AE于D，CE⊥AE于E．

（1）当直线AE处于如图①的位置时，有BD=DE+CE，请说明理由；

（2）当直线AE处于如图②的位置时，则BD、DE、CE的关系如何？请说明理由；

（3）归纳（1）、（2），请用简洁的语言表达BD、DE、CE之间的关系．

 

 

Answer 1

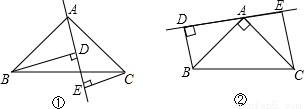
（1）见解析 （2）见解析 （3）BD=DE-CE

【解析】此题考查了全等三角形的判定与性质，以及等腰直角三角形的性质，利用了转化及等量代换的思想，熟练掌握全等三角形的判定与性质是解本题的关键．

（1）由BD垂直于AE，得到三角形ABD为直角三角形，利用直角三角形两锐角互余得到一对角互余，再由∠BAC=90°，得到一对角互余，利用同角的余角相等得到一对角相等，再由一对直角相等，AB=AC，利用AAS可得出三角形ABD与三角形ACE全等，由全等三角形的对应边相等得到AD=CE，BD=AE，由AE=AD+DE，等量代换即可得证；

（2）当直线AE处于如图②的位置时，则BD、DE、CE的关系为BD=DE-CE，理由为：同（1）得出三角形ABD与三角形ACE全等，由全等三角形的对应边相等得到AD=CE，BD=AE，由AE=DE-AD等量代换即可得证；

（3）由（1）（2）总结得到当D、E位于直线BC异侧时，BD=DE+CE；当D、E位于直线BC同侧时，BD=DE-CE．

【解析】
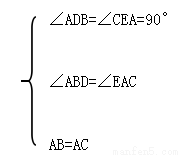
（1）证明：∵BD⊥AE，CE⊥AE，

∴∠BDA=∠AEC=90°，∴∠ABD+∠BAD=90°，

∵∠BAC=90°，∴∠BAD+∠EAC=90°∴∠ABD=∠EAC，

在△ABD和△CAE中

∵

∴△ABD≌△CAE（AAS）

∴AD=CE，BD=AE，

∵AE=AD+DE，

∴BD=DE+CE；

（2）BD、DE、CE的关系为BD=DE-CE，理由为：

证明：在△ABD和△CAE中

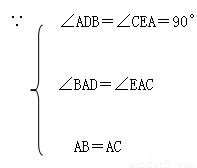
∴△ABD≌△CAE（AAS）

∴AD=CE，BD=AE，

∵AE=DE-AD，

∴BD=DE-CE；

（3）当D、E位于直线BC异侧时，BD=DE+CE；当D、E位于直线BC同侧时，BD=DE-CE．