
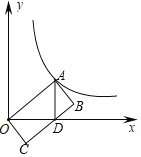
【题目】如图,在平面直角坐标系中,矩形![]() 的边
的边![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 轴,反比例函数
轴,反比例函数![]() 的图象经过点
的图象经过点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,![]() .
.
(1)求反比例函数的解析式;
(2)点![]() 为
为![]() 轴上一动点,当
轴上一动点,当![]() 的值最小时,求出点
的值最小时,求出点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据矩形的性质及等腰直角三角形得到OD=AD,即可求出A点坐标,故可求出反比例函数解析式;(2)过点![]() 作
作![]() 垂足为
垂足为![]() ,先求出
,先求出![]() 点坐标,
点坐标,
再求出点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,直线
,直线![]() 与
与![]() 轴的交点就是所求点
轴的交点就是所求点![]() ,此时
,此时![]() 最小,根据待定系数法确定直线AB1的关系式,再求出与y轴的交点即为所求.
最小,根据待定系数法确定直线AB1的关系式,再求出与y轴的交点即为所求.
解:(1)∵![]() 是矩形,
是矩形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() 轴,
轴,
∴![]() ,
,
∴![]() ,
,
∵![]()
∴![]() ,即
,即![]()
把点 ![]() 代入的
代入的![]() 得,
得,![]()
∴反比例函数的解析式为:![]() .
.
答:反比例函数的解析式为:![]() .
.
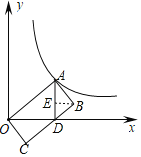
(2)过点![]() 作
作![]() 垂足为
垂足为![]() ,
,
∵![]() ,
,![]() ,
,![]()
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
则点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,直线
,直线![]() 与
与![]() 轴的交点就是所求点
轴的交点就是所求点![]() ,此时
,此时![]() 最小,
最小,
设直线AB1的关系式为![]() ,将
,将 ![]() ,
,![]() ,代入得,
,代入得,
 解得:
解得:![]() ,
,![]() ,
,
∴直线![]() 的关系式为
的关系式为![]() ,
,
当![]() 时,
时,![]() ,
,
∴点![]()
答:点![]() 的坐标为
的坐标为![]() .
.


科目:初中数学 来源: 题型:
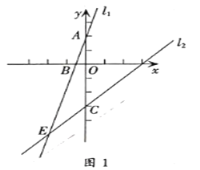
【题目】如图1,在直角坐标系中,一次函数的图象![]() 与
与![]() 轴交于点
轴交于点![]() ,与一次函数
,与一次函数![]() 的图象
的图象![]() 交于点
交于点![]() .
.
(1)求![]() 的值及
的值及![]() 的表达式;
的表达式;
(2)直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,求四边形
,求四边形![]() 的面积;
的面积;
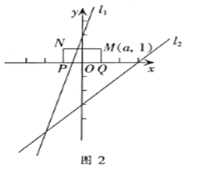
(3)如图2,已知矩形![]() ,
,![]() ,
,![]() ,
,![]() ,矩形
,矩形![]() 随边
随边![]() 在
在![]() 轴上平移而移动,若矩形
轴上平移而移动,若矩形![]() 与直线
与直线![]() 或
或![]() 有交点,直接写出
有交点,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
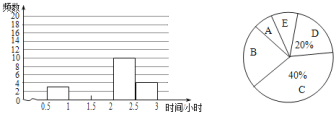
【题目】某校开展了为期一周的“新时代文明实践”活动,为了解情况,学生会随机调查了部分学生在这次活动中“宣传文明礼仪”的时间,并将统计的时间(单位:小时)分成5组,A:0.5≤x<1,B;1≤x<1.5,C:1.5≤x<2,D:2≤x<2.5,E:2.5≤x<3,制作成两幅不完整的统计图(如图).
请根据图中提供的信息,解答下列问题:
(1)学生会随机调查了 名学生.
(2)补全频数分布直方图.
(3)若全校有900名学生,估计该校在这次活动中“宣传文明礼仪”的时间不少于2小时的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店准备购进![]() 两种商品,
两种商品,![]() 种商品毎件的进价比
种商品毎件的进价比![]() 种商品每件的进价多20元,用3000元购进
种商品每件的进价多20元,用3000元购进![]() 种商品和用1800元购进
种商品和用1800元购进![]() 种商品的数量相同.商店将
种商品的数量相同.商店将![]() 种商品每件的售价定为80元,
种商品每件的售价定为80元,![]() 种商品每件的售价定为45元.
种商品每件的售价定为45元.
(1)![]() 种商品每件的进价和
种商品每件的进价和![]() 种商品每件的进价各是多少元?
种商品每件的进价各是多少元?
(2)商店计划用不超过1560元的资金购进![]() 两种商品共40件,其中
两种商品共40件,其中![]() 种商品的数量不低于
种商品的数量不低于![]() 种商品数量的一半,该商店有几种进货方案?
种商品数量的一半,该商店有几种进货方案?
(3)端午节期间,商店开展优惠促销活动,决定对每件![]() 种商品售价优惠
种商品售价优惠![]() (
(![]() )元,
)元,![]() 种商品售价不变,在(2)条件下,请设计出销售这40件商品获得总利润最大的进货方案.
种商品售价不变,在(2)条件下,请设计出销售这40件商品获得总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一条公路旁依次有![]() 三个村庄,甲乙两人骑自行车分别从
三个村庄,甲乙两人骑自行车分别从![]() 村、
村、![]() 村同时出发前往
村同时出发前往![]() 村,甲乙之间的距离
村,甲乙之间的距离![]() 与骑行时间
与骑行时间![]() 之间的函数关系如图所示,下列结论:①
之间的函数关系如图所示,下列结论:①![]() 两村相距10
两村相距10![]() ;②出发1.25
;②出发1.25![]() 后两人相遇;③甲每小时比乙多骑行8
后两人相遇;③甲每小时比乙多骑行8![]() ;④相遇后,乙又骑行了15
;④相遇后,乙又骑行了15![]() 或65
或65![]() 时两人相距2
时两人相距2![]() .其中正确的个数是( )
.其中正确的个数是( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线L:![]() 经过点A(-3,0)和点B(0,-6),L关于原点O对称的抛物线为
经过点A(-3,0)和点B(0,-6),L关于原点O对称的抛物线为![]() .
.
(1)求抛物线L的表达式;
(2)点P在抛物线![]() 上,且位于第一象限,过点P作PD⊥y轴,垂足为D.若△POD与△AOB相似,求符合条件的点P的坐标.
上,且位于第一象限,过点P作PD⊥y轴,垂足为D.若△POD与△AOB相似,求符合条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数![]() 的图象记为
的图象记为![]() ,函数
,函数![]() 的图象记为
的图象记为![]() ,其中
,其中![]() 为常数,
为常数,![]() 与
与![]() 合起来的图象记为
合起来的图象记为![]() .
.
(Ⅰ)若![]() 过点
过点![]() 时,求
时,求![]() 的值;
的值;
(Ⅱ)若![]() 的顶点在直线
的顶点在直线![]() 上,求
上,求![]() 的值;
的值;
(Ⅲ)设![]() 在
在![]() 上最高点的纵坐标为
上最高点的纵坐标为![]() ,当
,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
动手操作:
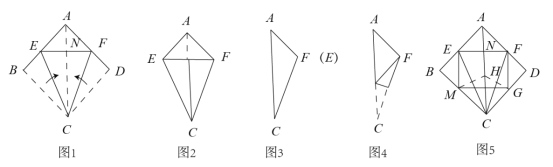
第一步:如图1,正方形纸片ABCD沿对角线AC所在直线折叠,展开铺平.在沿过点C的直线折叠,使点B,点D都落在对角线AC上.此时,点B与点D重合,记为点N,且点E,点N,点F三点在同一直线上,折痕分别为CE,CF.如图2.
第二步:再沿AC所在的直线折叠,△ACE与△ACF重合,得到图3
第三步:在图3的基础上继续折叠,使点C与点F重合,如图4,展开铺平,连接EF,FG,GM,ME,如图5,图中的虚线为折痕.
问题解决:
(1)在图5中,∠BEC的度数是 ,![]() 的值是 ;
的值是 ;
(2)在图5中,请判断四边形EMGF的形状,并说明理由;
(3)在不增加字母的条件下,请你以图中5中的字母表示的点为顶点,动手画出一个菱形(正方形除外),并写出这个菱形: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com