
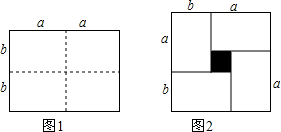
分析 (1)根据阴影部分的面积=边长为a+b的正方形的面积-长为2a,宽为2b的长方形的面积;
(2)除第(1)小题的方法外,还可以用正方形的面积减4个长方形的面积即可;
(3)借助第(2)小题的结论,即可找到三个式子之间的关系;
(4)利用(3)中的结论,利用整体代入即可.
解答 解:(1)阴影部分的面积为:(a+b)2-2a×2b=a2+2ab+b2-4ab=a2-2ab+b2=(a-b)2;
(2)方法1:(a+b)2-2a×2b=a2+2ab+b2-4ab=a2-2ab+b2=(a-b)2;
方法2:(a+b)2-4•a•b=a2+2ab+b2-4ab=a2-2ab+b2=(a-b)2;
(3)根据第(2)小题,可以看出,(a+b)2=(a-b)2+4ab;
(4)根据(3)中的结论,可知:(m+n)2=(m-n)2+4mn=(-7)2+4×5=49+20=69.
故答案为:(1)(a-b)2;(2)(a+b)2-2a•2b=(a-b)2;(a+b)2-4•ab=(a-b)2;(3)(a+b)2=(a-b)2+4ab;(4)69.
点评 本题主要考查完全平方公式,熟记完全平方公式、图形的面积是解决此题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
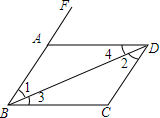 按图填空,并在横线内标明理由:
按图填空,并在横线内标明理由:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 2013 | B. | 2014 | C. | 2015 | D. | 2016 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为点E,AE=BE.
已知:如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为点E,AE=BE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
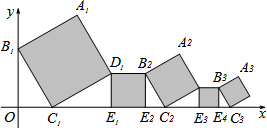 已知在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在y轴上,点C1,E1,E2,C2,E3,E4,C3在x轴上.若正方形A1B1C1D1的边长为2,∠B1C1O=60°,B1C1∥B2C2∥B3C3,则点A3到x轴的距离是( )
已知在平面直角坐标系中放置了5个如图所示的正方形(用阴影表示),点B1在y轴上,点C1,E1,E2,C2,E3,E4,C3在x轴上.若正方形A1B1C1D1的边长为2,∠B1C1O=60°,B1C1∥B2C2∥B3C3,则点A3到x轴的距离是( )| A. | $\frac{1+\sqrt{3}}{9}$ | B. | $\frac{3+\sqrt{3}}{9}$ | C. | $\frac{3+\sqrt{3}}{3}$ | D. | $\frac{1+\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2-$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | -$\sqrt{3}$ | D. | 2$+\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com