
【题目】已知,四边形![]() 是正方形,点
是正方形,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 的延长线上,且
的延长线上,且![]() ,连接
,连接![]() .
.
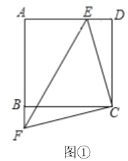
(1)如图①,连接![]() .求证:
.求证:![]() 是等腰直角三角形;
是等腰直角三角形;
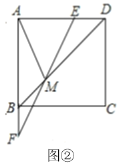
(2)如图②,![]() 与
与![]() 交于点
交于点![]() ,若正方形
,若正方形![]() 的边长为6,
的边长为6,![]() ,求
,求![]() 的长.
的长.
(3)点![]() ,点
,点![]() 分别在边
分别在边![]() ,边
,边![]() 上,
上,![]() 与
与![]() 交于点
交于点![]() ,且
,且![]() ,若正方形
,若正方形![]() 的边长为6.
的边长为6.![]() 求
求![]() 的长(直接写出结果即可)
的长(直接写出结果即可)
【答案】(1)见解析;(2)![]() ;(3)3
;(3)3
【解析】
(1)证明△CDE≌△CBF即可得出结论;
(2)过![]() 作
作![]() 于
于![]() ,构建直角△AGM,证明△FGM∽△FAE,得FG=2GM,设GM=x,则FG=2x,根据正方形的性质可得△BGM是等腰直角三角形,则可求出AG=4,GM=2,由勾股定理可得AM的长;
,构建直角△AGM,证明△FGM∽△FAE,得FG=2GM,设GM=x,则FG=2x,根据正方形的性质可得△BGM是等腰直角三角形,则可求出AG=4,GM=2,由勾股定理可得AM的长;
(3)过G作GP⊥CD于P,证明△GHP≌△CED,可得CE=GH=![]() ,在
,在![]() 中利用勾股定理可求得DE的长.
中利用勾股定理可求得DE的长.
解:(1)∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中, ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是等腰直角三角形;
是等腰直角三角形;
(2)如图,过![]() 作
作![]() 于
于![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,
∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;

(3)如图,过![]() 作
作![]() 于
于![]() ,
,
由(1)知:![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
在![]() 中,由勾股定理得:
中,由勾股定理得:![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是直径,CD是弦,AB⊥CD,垂足为E,连结CO,AD,∠BAD=20°,则下列说法中正确的是( )
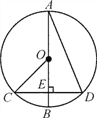
A. ∠BOC=2∠BAD B. CE=EO C. ∠OCE=40° D. AD=2OB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把八个完全相同的小球平分为两组,每组中每个分别写上1,2,3,4四个数字,然后分别装入不透明的口袋内搅匀,从第一个口袋内取出一个数记下数字后作为点P的横坐标x,然后再从第二个口袋中取出一个球记下数字后作为点P的纵坐标,则点P(x,y)落在直线y=﹣x+5上的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校要从数学竞赛初赛成绩相同的四名学生(其中2名男生,2名女生)中,随机选出2名学生去参加决赛,则选出的2名学生恰好为1名男生和1名女生的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
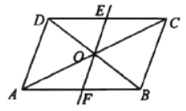
【题目】如图,![]() 的对角线
的对角线![]() 、
、![]() 相交于点
相交于点![]() ,对角线
,对角线![]() 绕点
绕点![]() 逆时针旋转,分别交边
逆时针旋转,分别交边![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,
,![]() .当
.当![]() 绕点
绕点![]() 逆时针方向旋转
逆时针方向旋转![]() 时,判断四边形
时,判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上的一动点(点
边上的一动点(点![]() 与
与![]() 、
、![]() 点不重合),四边形
点不重合),四边形![]() 沿
沿![]() 折叠得边形
折叠得边形![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() .
.
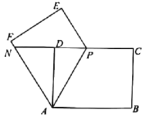
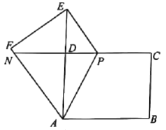
图① 图②
(1)求证:![]() ;
;
(2)如图②,若点![]() 恰好在
恰好在![]() 的延长线上时,试求出
的延长线上时,试求出![]() 的长度;
的长度;
(3)当![]() 时,求证:
时,求证:![]() 是等腰三角形.
是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在矩形![]() 中,把
中,把![]() 、
、![]() 分别翻折,使点
分别翻折,使点![]() 、
、![]() 分别落在对角线
分别落在对角线![]() 上的点
上的点![]() 、
、![]() 处,折痕分别为
处,折痕分别为![]() 、
、![]() .
.
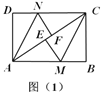
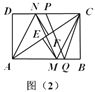
(1)求证:![]() .
.
(2)请连接![]() 、
、![]() ,证明四边形
,证明四边形![]() 是平行四边形
是平行四边形
(3)![]() 、
、![]() 是矩形的边
是矩形的边![]() 、
、![]() 上的两点,连结
上的两点,连结![]() 、
、![]() 、
、![]() ,如图(2)所示,若
,如图(2)所示,若![]() ,
,![]() .且
.且![]() ,
,![]() ,求
,求![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
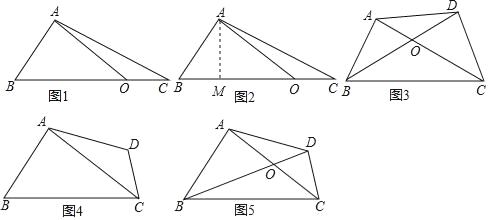
【题目】问题提出:某物业公司接收管理某小区后,准备进行绿化建设,现要将一块四边形的空地(如图5,四边形ABCD)铺上草皮,但由于年代久远,小区规划书上该空地的面积数据看不清了,仅仅留下两条对角线AC,BD的长度分别为20cm,30cm及夹角∠AOB为60°,你能利用这些数据,帮助物业人员求出这块空地的面积吗?
问题显然,要求四边形ABCD的面积,只要求出△ABD与△BCD(也可以是△ABC与△ACD)的面积,再相加就可以了.
建立模型:我们先来解决较简单的三角形的情况:
如图1,△ABC中,O为BC上任意一点(不与B,C两点重合),连接OA,OA=a,BC=b,∠AOB=α(α为OA与BC所夹较小的角),试用a,b,α表示△ABC的面积.
解:如图2,作AM⊥BC于点M,
∴△AOM为直角三角形.
又∵∠AOB=α,∴sinα=![]() 即AM=OAsinα
即AM=OAsinα
∴△ABC的面积=![]() BCAM=
BCAM=![]() BCOAsinα=
BCOAsinα=![]() absinα.
absinα.
问题解决:请你利用上面的方法,解决物业公司的问题.
如图3,四边形ABCD中,O为对角线AC,BD的交点,已知AC=20m,BD=30m,∠AOB=60°,求四边形ABCD的面积.(写出辅助线作法和必要的解答过程)
新建模型:若四边形ABCD中,O为对角线AC,BD的交点,已知AC=a,BD=b,∠AOB=α(α为OA与BC所夹较小的角),直接写出四边形ABCD的面积= .
模型应用:如图4,四边形ABCD中,AB+CD=BC,∠ABC=∠BCD=60°,已知AC=a,则四边形ABCD的面积为多少?(“新建模型”中的结论可直接利用)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com